Addition

Pronunciation: /əˈdɪ.ʃən/ Explain

Addition is joining two or more quantities together to make a sum. Figure 1 gives an example of integer addition. In the addition statement 4 + 3 = 7, 4 and 3 are addends and 7 is the sum. Addends are what is being added together, and the sum is the result of the addition. The symbol '+' is called the addition sign.

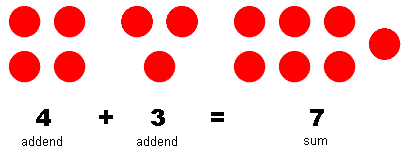Figure 1: Representation of 4 + 3 = 7

Real numbers can also be added. Figure 2 gives a representation of 2 + 1 = 3.

Figure 2: Representation of 2 + 1 = 3

Manipulative 3 represents the addition of real numbers. Click on the blue points and drag them to change the figure.

Click on the points A and B near the top to change the figure. The blue and red arrows on the number line show A added to B. The sum A+B is below them in purple.

Manipulative 1 - Addition Created with GeoGebra.

Addition is also defined for many types of math entities such as vectors and matrices.

Subtraction

Mathematicians usually define subtraction as adding the additive inverse of a value. Subtraction is defined this way so that subtraction of vectors and matrices and other math entities makes more sense. Stated mathematically, a - b ≡ a + ^-b. A difference is the result of subtracting one number from another. For example, in the equation 7 - 4 = 3, 3 is the difference.

A example of this is 5 - 4 = 5 + ^-4 = 1

Properties of Addition of Real and Complex Numbers

Property Name	Example	Description
Additive property of zero Additive identity	a + 0 = 0 + a = a	Any number plus zero equals the original number. 0 is the additive identity for real and complex numbers.
Additive inverse	a + (-a) = 0	The additive inverse of any real or complex number is the negative of that numbers.
Associative property of addition	a + ( b + c ) = ( a + b ) + a	The order of in which multiple additions of real and complex numbers are performed does not change the result.
Commutative property of addition	a + b = b + a	It doesn't matter which of two numbers come first in addition of real and complex numbers.
Distributive Property of Multiplication over Addition and Subtraction	a ( b + c ) = ab + ac, and a ( b - c ) = ab - ac	Multiplication is distributive over addition and subtraction.
Additive property of equality	If a = b then a + c = b + c.	The additive property of equality states that any number can be added to both sides of an equation without changing the truth value of the equation.
Subtractive property of equality	If a = b then a - c = b - c.	The subtractive property of equality states that any number can be subtracted from both sides of an equation without changing the truth value of the equation.
Table 1: Properties of Addition

Addition Facts

Addition facts are two operands and the result of adding those two operands. The following table gives the addition facts for 0 through 10.

+	0	1	2	3	4	5	6	7	8	9	10
0	0	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10	11
2	2	3	4	5	6	7	8	9	10	11	12
3	3	4	5	6	7	8	9	10	11	12	13
4	4	5	6	7	8	9	10	11	12	13	14
5	5	6	7	8	9	10	11	12	13	14	15
6	6	7	8	9	10	11	12	13	14	15	16
7	7	8	9	10	11	12	13	14	15	16	17
8	8	9	10	11	12	13	14	15	16	17	18
9	9	10	11	12	13	14	15	16	17	18	19
10	10	11	12	13	14	15	16	17	18	19	20

How to Add Complex Numbers

To add two complex numbers, add the corresponding parts. Given two complex numbers a + bi and c + di, (a + bi) + (c + di) = (a + c) + (b + d)i. Example: (3 - 2i) + (-1 + 3i) = (3 + (-1)) + (-2 + 3)i = 2 + 1i = 2 + i.

References

1. McAdams, David E.. All Math Words Dictionary, addition. 2nd Classroom edition 20150108-4799968. pg 10. Life is a Story Problem LLC. January 8, 2015. Buy the book

Educator Resources

• McAdams, David E.. Addition of Integers Classroom Demonstrator. allmathwords.org. 12/24/2009. https://allmathwords.org/en/a/addtionintegers_cd.html.
• McAdams, David E.. Addition of Real Numbers Classroom Demonstrator. allmathwords.org. 12/24/2009. https://allmathwords.org/en/a/additionreal_cd.html.
• Addition. www.mathsisfun.com. Math Is Fun. 6/18/2018. https://www.mathsisfun.com/numbers/addition.html.

Cite this article as:

McAdams, David E. Addition. 4/5/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/a/addition.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/5/2019: Updated formating of equations. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/12/2018: Removed broken links, changed Geogebra links to work with Geogebra 5, updated license, implemented new markup. (McAdams, David E.)
10/12/2010: Added "Adding complex numbers", additive identity, additive inverse, and additive property of equality. (McAdams, David E.)
1/4/2010: Added "References". (McAdams, David E.)
3/3/2009: Added discussion of difference to the section on subtraction. (McAdams, David E.)
9/16/2008: Changed figure 3 to a manipulative. (McAdams, David E.)
6/7/2008: Corrected spelling errors. (McAdams, David E.)
5/14/2008: Initial version. (McAdams, David E.)