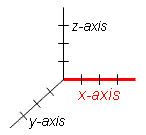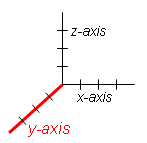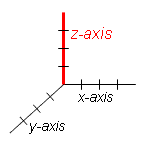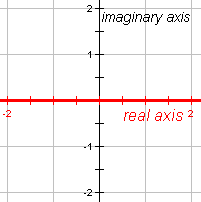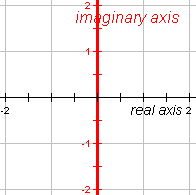Axis
Pronunciation: /ˈæk.sɪs/ Explain--plural axes
An axis is a line that is used as a reference for drawing a figure.[2] This line can exist in two dimensional and three or more dimensional space. It can also be used as a reference for geometric reflections.
Common Axes
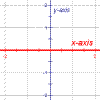
x-Axis | |||||
|
The x-axis is the horizontal axis on a two variable Cartesian graph. This axis is typically assigned to the input of the function being represented. This also means that the x-axis typically represents the independent variable. | ||||
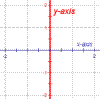
y-Axis | |||||
|
The y-axis is the vertical axis on a two variable Cartesian graph. The y-axis is typically assigned to the output of the function being represented. This also means that the y-axis typically represents the dependent variable. On a three-variable Cartesian system, the y-axis typically represents an independent variable. | ||||
z-Axis | |||||
|
The z-axis is the third axis on a three variable Cartesian graph. The z-axis is typically assigned to the output of the function being graphed. This also means that it shows the dependent variable. | ||||
Axis of Symmetry | |||||
|
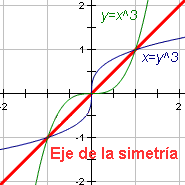
An axis of symmetry is the line around which a curve is symmetrical.[4] For parabolas this is a line which passes through the vertex (see figure 6). Functions and their inverses can also be drawn using the axis of symmetry, which is the line with the equation y = x (see figure 7). | ||||
Real Axis | |||||
|
In the complex plane, the real axis, on which real numbers are represented, is the horizontal axis.[3] | ||||
Imaginary Axis | |||||
|
In the complex plane, the imaginary axis, on which imaginary numbers are represented, is the vertical axis.[3] | ||||
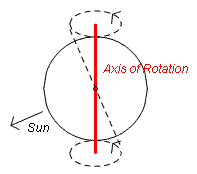
Axis of Rotation | |||||
|
An axis of rotation is a line about which a geometric object rotates.[5] The earth is an example of a rotating sphere. The line from the north pole to the south pole is the axis of rotation as show in figure 10. The earth spins, or rotates, about the axis of rotation. | ||||
References
- McAdams, David E.. All Math Words Dictionary, axis. 2nd Classroom edition 20150108-4799968. pg 23. Life is a Story Problem LLC. January 8, 2015. Buy the book
- Hustler, James Devereux. The Elements of the Conic Sections with the Sections of the Conoids. 3rd edition. pp 1-18. www.archive.org. Published by J. Deighton and Sons. 1826. Last Accessed 6/12/2018. http://www.archive.org/stream/elementsofconics00hastuoft#page/1/mode/1up/search/axis. Buy the book
- Turnbull, H. W., M.A. F.R.S.. Theory of Equations. 4th edition. pp 6-7. www.archive.org. Oliver and Lloyd. 1947. Last Accessed 6/12/2018. http://www.archive.org/stream/theoryofequation029153mbp#page/n23/mode/1up/search/axis. Buy the book
- Bettinger, Alvin K. and Englund, John A.. Algebra and Trigonometry. pp 49-50. www.archive.org. International Textbook Company. January 1963. Last Accessed 6/12/2018. http://www.archive.org/stream/algebraandtrigon033520mbp#page/n66/mode/1up/search/axis. Buy the book
Cite this article as:
McAdams, David E. Axis. 12/21/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/a/axis.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)6/13/2018: Removed broken links, updated license, implemented new markup.. (McAdams, David E.)
1/8/2010: Added "References". (McAdams, David E.)
6/19/2008: Corrected imaginary axis text, added hot link to complex plane. (McAdams, David E.)
6/7/2008: Corrected spelling. (McAdams, David E.)
3/11/2008: Added vocabulary links. Corrected typo in y-axis (McAdams, David E.)
8/10/2007: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License