Boolean Algebra

Pronunciation: /ˈbu.li.ən ˈæl.dʒə.brə/ Explain

Boolean algebra is an algebra where there are only two values, typically represented by 1 or 0.^[2][3] If the elements are truth values, 1 represents 'true', and 0 represents 'false'.

In boolean algebra, there are four commonly used operators: ∧ (and), ∨ (or), ⊖ (exclusive or), and ¬ (negation, not, or complement). Table 1 summarizes the boolean operators.

Operator	Name	Truth Table	Venn Diagram	Description
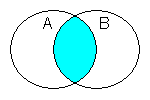
∧	and	A B A ∧ B 0 0 0 0 1 0 1 0 0 1 1 1		∧ returns true (1) if both operands are true (1), otherwise it returns false (0). In most computer languages, and is represented by '&' or '&&'. The operator '^' represents exponentiation in most computer languages.
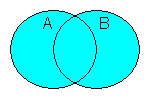
∨	or	A B A ∨ B 0 0 0 0 1 1 1 0 1 1 1 1		∨ returns true (1) if one or both operands are true (1), otherwise it returns false (0). In most computer languages, or is represented by '|' or '||'.
¬	not	A ¬A 0 1 1 0		¬ returns true (1) if the operand is false (0), and false (0) if the operand is true (1). In most computer languages negate or not is represented by the exclamation mark '!'.
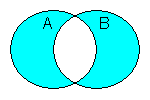
⊖	exclusive or	A B A ⊖ B 0 0 0 0 1 1 1 0 1 1 1 0		⊖ returns true (1) if one but not both operands are true (1), otherwise it returns false (0). In most computer languages, exclusive or is implemented as a function call.
Table 1: Truth table for boolean operators.

Properties of Operations

Commutative

The three binary operators are commutative:
a∧b = b∧a
a∨b = b∨a
a⊖b = b⊖a.

Associative

The three binary operators are associative:
a ∧ (b ∧ c) = (a ∧ b) ∧ c
a ∨ (b ∨ c) = (a ∨ b) ∨ c
a ⊖ (b ⊖ c) = (a ⊖ b) ⊖ c.

Distributive

The 'and' and 'or' operators are mutually distributive:
a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c)
a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c).

References

1. McAdams, David E.. All Math Words Dictionary, Boolean algebra. 2nd Classroom edition 20150108-4799968. pg 27. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. boolean. merriam-webster.com. Encyclopedia Britannica. Merriam-Webster. Last Accessed 6/19/2018. http://www.merriam-webster.com/dictionary/boolean. Buy the book
3. Boole, George. The Mathematical Analysis of Logic. www.archive.org. Macmillan, Barclay and Macmillan. 1847. Last Accessed 6/19/2018. http://www.archive.org/stream/mathematicalanal00booluoft#page/n6/mode/1up. Buy the book
4. Couturat, Louis. The Algebra of Logic. Translated by Lydia Gillingham Robinson, B. www.archive.org. A.. Open Court Publishing. 1914. Last Accessed 6/19/2018. http://www.archive.org/stream/algebralogicbylc00coutrich#page/n5/mode/1up. Buy the book

More Information

• Boolean Algebra. www.tutorialspoint.com. Tutorials Point. 6/21/2018. https://www.tutorialspoint.com/computer_logical_organization/boolean_algebra.htm.

Cite this article as:

McAdams, David E. Boolean Algebra. 4/12/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/b/booleanalgebra.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/12/2019: Changed equations and expressions to new format. (McAdams, David E.)
1/29/2019: Corrected illustrations. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/22/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
6/30/2008: Added Venn diagrams. (McAdams, David E.)
4/22/2008: Initial version. (McAdams, David E.)