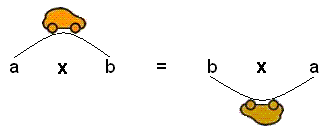Commutative Property of Multiplication

Pronunciation: /kəˈmjuːtteɪ.tɪv ˈprɒp.ər.ti ʌv ˌmʌl.tə.plɪˈkeɪ.ʃən/ Explain

The commutative property of multiplication states that multiplying two numbers will get the same result no matter which number comes first.^[1] The order in which two numbers are multiplied does not change the product. This is expressed by the equation: a·b = b·a.

Figure 1: Commutative property of multiplication cartoon

One way to remember the commutative property of multiplication is to use the root word, 'commute'. Commute means to travel from one place to another, such as commuting to work. As diagrammed in figure 1, in the commutative property of multiplication, the variable 'a' commutes to where the 'b' was, and the variable 'b' commutes to where the 'a' was.

Figure 2 - Representation of 2·3 = 3·2 using dots.

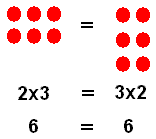
Figure 2 is a representation of the commutative property of multiplication using dots. On the left is a rectangle showing 2·3. On the right is a rectangle showing 3·2. Both have six dots in them. You can transform the first into the second by turning the first on its side.

Click on the points and drag them to change the figure. Can you find a case where A·B does not equal B·A? Manipulative 1 - Commutative Property of Multiplication Created with GeoGebra.

Manpulative 1 is a representation of the commutative property of multiplication that uses the length of a line segment to represent each number, and right angles to represent multiplication. Notice that when we 'multiply' one by the other, it doesn't matter which comes first, the total area is the same. Click on the yellow points of the two lines on top and drag the points. Dragging these points changes the diagram showing that, for any values of 'a' and 'b', this property holds true.

References

1. McAdams, David E.. All Math Words Dictionary, Commutative Property of Multiplication. 2nd Classroom edition 20150108-4799968. pg 38. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. commutative. merriam-webster.com. Encyclopedia Britannica. Merriam-Webster. Last Accessed 6/25/2018. http://www.merriam-webster.com/dictionary/commutative. Buy the book
3. Jones, Burton. Elementary Concepts of Mathematics. pp 31-34. www.archive.org. MacMillan and Company. 1947. Last Accessed 6/25/2018. http://www.archive.org/stream/elementaryconcep029487mbp#page/n52/mode/1up/search/commutative. Buy the book
4. Bettinger, Alvin K. and Englund, John A.. Algebra and Trigonometry. pg 2. www.archive.org. International Textbook Company. January 1963. Last Accessed 6/25/2018. http://www.archive.org/stream/algebraandtrigon033520mbp#page/n18/mode/1up. Buy the book
5. Fine, Henry B., Ph. D.. Number-System of Algebra Treated Theoretically and Historically. 2nd edition. pg 5. www.archive.org. D. C. Heath & Co., Boston, U.S.A.. 1907. Last Accessed 6/25/2018. http://www.archive.org/stream/thenumbersystemo17920gut/17920-pdf#page/n14/mode/1up/search/commutative. Buy the book

More Information

• McAdams, David E.. Commutative. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 6/27/2018. https://www.allmathwords.org/en/c/commutative.html.

Cite this article as:

McAdams, David E. Commutative Property of Multiplication. 4/13/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/c/commutemult.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

3/6/2019: Renamed Figure 3 as Manipulative 1. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/25/2018: Removed broken links, updated license, implemented new markup, updated GeoGebra apps. (McAdams, David E.)
12/19/2009: Added "References". (McAdams, David E.)
7/7/2008: Changed manipulative from Geometer's Sketchpad to GeoGebra. Corrected spelling (McAdams, David E.)
3/25/2008: Revised More Information to match current standard. (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)