Complex Number
Pronunciation: /kəmˈplɛks nʌm.bər/ ExplainA complex number is a number that contains two parts: a
real part and an 'imaginary' part. The real part is any real number. The imaginary
part is a real number multiplied by the imaginary unit
written as the lower-case letter 'i'. The imaginary unit
i represents
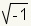 .
.
Complex numbers are typically written in the form
a + bi
where a is the real part and bi is
the imaginary part.
a + bi
can also be written
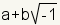 or
or
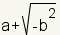
An imaginary number is a complex number with no real part,
such as
 or 6.2i.
This is sometimes called a pure imaginary number.
or 6.2i.
This is sometimes called a pure imaginary number.
 Understanding Check
Understanding Check
Classifying NumbersFor each number, decide which class or classes to which each number belongs. Click 'yes' or 'no' under each class of numbers. A number may belong to more than one class. |
|||
| Number | Complex | Real | Pure Imaginary |
|---|---|---|---|
| 6-6i | yes noYes is correct. 6-6i has a real part (6) and an imaginary part (-6i).No is incorrect. 6-6i has a real part (6) and an imaginary part (-6i). | yes noYes is incorrect. -6i is the imaginary part. A real number has no imaginary part so 6-6i is not a real number.No is correct. -6i is the imaginary part. A real number has no imaginary part so 6-6i is not a real number. | yes noYes is incorrect. 6-6i has a real part (6). An imaginary number has no real part so 6-6i is not a imaginary number.No is correct. 6-6i has a real part (6). An imaginary number has no real part so 6-6i is not a imaginary number. |
| 5 | yes noYes is correct. 5 has a real part (5). The imaginary part is (0i). All real numbers are also complex numbers.No is incorrect. 5 has a real part (5). The imaginary part is (0i). All real numbers are also complex numbers. | yes noYes is correct. 5 is the real part. While the imaginary part can be considered to be 0i, a complex number with 0i is also a real number.No is incorrect. 5 is the real part. While the imaginary part can be considered to be 0i, a complex number with 0i is also a real number. | yes noYes is incorrect. 5 has a real part (5). An imaginary number has no real part so 5 is not a imaginary number.No is correct. 5 has a real part (5). An imaginary number has no real part so 5 is not a imaginary number. |
| 2i | yes noYes is correct. 2i has an imaginary part (2i). The real part is (0). All pure imaginary numbers are also complex numbers.No is incorrect. 2i has an imaginary part (2i). The real part is (0). All imaginary numbers are also complex numbers. | yes noYes is incorrect. 2i has an imaginary part. A real number has no imaginary part, so 2i can not be imaginary.No is correct. 2i has an imaginary part. A real number has no imaginary part, so 2i can not be real. | yes noYes is correct. 2i has an imaginary part (2i). Since it has no real part, 2i is an imaginary number.No is incorrect. 2i has an imaginary part (2i). Since it has no real part, 2i is an imaginary number. |
| -3+4x | yes noYes is incorrect. -3+4x is an expression, not a number.No is correct. -3+4x is an expression, not a number. | yes noYes is incorrect. -3+4x is an expression, not a number.No is correct. -3+4x is an expression, not a number. | yes noYes is incorrect. -3+4x is an expression, not a number.No is correct. -3+4x is an expression, not a number. |
| Table 1: Classifying numbers | |||
Complex Plane
|
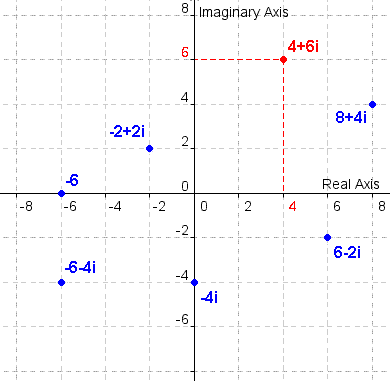
Complex numbers can be represented as points on the complex plane. Like the Cartesian plane, the complex plane has two axes: the real axis and the imaginary axis. The real axis is the horizontal axis. The real axis is also the real number line, put into the complex plane. The vertical axis is the imaginary axis. The complex plane is also called an Argand diagram. In figure 1, find the point 4+6i, which is red. Note that it corresponds to 4 on the real axis and 6 on the imaginary axis. Each point is plotted the same way. If a number has no imaginary part, it is a real number, and is found on the real axis. In figure 1, -6 is a real number on the real axis. If a number is an imaginary number, it is found on the imaginary axis. The number -4i in figure 1 is an example of an imaginary number on the imaginary axis. |
Powers of i
|
When simplifying expressions containing the imaginary constant
i, it is important to know the values of the integral
powers of i. To understand this, remember the definition of
i:
 .
Since the square root function is the inverse of the square function, .
Since the square root function is the inverse of the square function,
 .
So, .
So,
 .
Table 1 gives the values of the first five integral powers of i.
Can you figure out the next three? Come up with your answer, then click on 'Click for answer'
to check your answer. .
Table 1 gives the values of the first five integral powers of i.
Can you figure out the next three? Come up with your answer, then click on 'Click for answer'
to check your answer.
|
| ||||||||||||||||||||||
How To Add Complex Numbers
When adding complex numbers, add
corresponding
parts. Add the real parts together and the imaginary parts together:
a+bi + c+di = (a+c)+(b+d)i
Here are some examples:
3+2i + 1-3i = (3+1)+(2-3)i = 4-1i = 4-i
4+1i + -2+2i = (4-2)+(1+2)i = 2+3i
How to Multiply Complex Numbers
| To multiply complex numbers, cross multiply the parts: |
| ×(a+bi) |
| ×(c+di) |
| ×(a·c + bi·c |
| ×(a·c + a·di + bi·di |
| +ac + (ad + bc)i + bdi2 |
| It is important to remember that i2 = -1. Substitute -1 for i2 in the equation: |
| = ac + (ad + bc)i + bd·(-1) |
| = ac + (ad + bc)i - bd· |
| = ac - bd + (ad + bc)i |
| Here is an example: |
| (1-3i)·(-6+2i) |
= 1·(-6)+1·2i+(-3)·(-6)i+(-3)·2i2 |
= -6+2i+18i-6i2 |
= -6+20i-6i2 |
| Substitute -1 for i2 in the equation: |
| -6+20i-6i2 |
| = -6+20i-6(-1) |
| = -6+20i+6 |
| = -6+6+20i |
| = 0+20i |
| = 20i |
Properties of Complex Numbers
| Property | Value | Example | Description |
|---|---|---|---|
| Additive Identity |

|
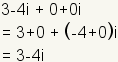
| The additive identity is the number that, when added to any complex number,
gives the original number unchanged. The additive identity for complex numbers is
 . . |
| Multiplicative Identity |
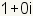
|
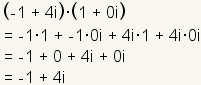
| The multiplicative identity is the number that, when multiplied by
any complex number, gives the original number unchanged. The multiplicative
identity for complex numbers is
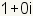 . . |
| Additive Inverse |
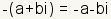
|
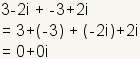
| The additive inverse of a complex number is the number that when added
to the original number gives the additive identity. The additive identity of
an arbitrary complex number 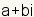 is
is 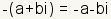 . . |
| Multiplicative Inverse |
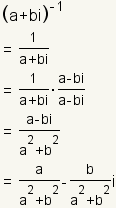
|
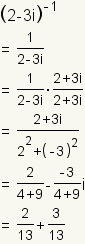
| The multiplicative inverse of a complex number is the number that when
multiplied by the original number gives the multiplicative identity. The
multiplicative inverse of an arbitrary complex number
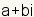 is is
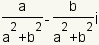 . . |
| Associate Property of Addition |
![(a+bi)+[(c+di)+(e+fi)]=[(a+bi)+(c+di)]+(e+fi)](../../equations/c/complexnumbereqn15.png)
|
![(2-3i) + [(5 + 2i) + (-3 - 6i)]= [(2-3i) + (5+2i)] + (-3-6i) implies (2-3i) + [2-4i]= [7-i] + (-3-6i) implies 4-7i=4-7i](../../equations/c/complexnumbereqn16.png)
| The associative property of addition states that the order in which complex numbers are added does not matter. |
| Commutative Property of Addition |
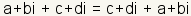
|
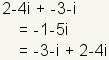
| The commutative property of addition states that addends of complex numbers can be switched without changing the result. |
| Associate Property of Multiplication |
![(a+bi)*[(c+di)*(e+fi)]=[(a+bi)*(c+di)]*(e+fi)](../../equations/c/complexnumbereqn19.png)
|
![(5+2i)*[(-3-6i)*(2-3i)]=[(5+2i)*(-3-6i)]*(2-3i) implies (5+2i)*(-24-3i)=(-3-36i)*(2-3i) implies -114-63i=-114-63i.](../../equations/c/complexnumbereqn20.png)
| The associative property of multiplication states that the order in which complex numbers are added does not matter. |
| Commutative Property of Multiplication |
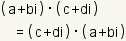
|
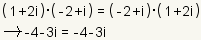
| The commutative property of multiplication states that multiplicands of complex numbers can be switched without changing the result. |
| Table 1: Properties of complex numbers. | |||
Addition
|
Click on the blue points and drag them to change the figure. |
| Manipulative 2 - Addition of Complex Numbers Created with GeoGebra. |
Additive Inverse
|
Click on the blue point and drag it to change the figure. What is the additive inverse of 2-1i? |
| Manipulative 3 - Additive Identity of a Complex Number Created with GeoGebra. |
Multiplicative Inverse
|
Click on the blue point and drag it to change the figure. What complex number has a multiplicative inverse of 1 + i? |
| Manipulative 4 - Multiplicative Inverse of a Complex Number Created with GeoGebra. |
References
- McAdams, David E.. All Math Words Dictionary, complex number. 2nd Classroom edition 20150108-4799968. pg 39. Life is a Story Problem LLC. January 8, 2015. Buy the book
Cite this article as:
McAdams, David E. Complex Number. 4/14/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/c/complexnumber.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/14/2019: Updated equations and expressions to new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/25/2018: Removed broken links, updated license, implemented new markup, updated GeoGebra apps. (McAdams, David E.)
1/8/2010: Added "References". (McAdams, David E.)
12/26/2008: Changed equations from html to images. (McAdams, David E.)
7/17/2008: Added addition, multiplication, and properties of complex numbers. (McAdams, David E.)
6/9/2008: Added paragraph on imaginary numbers. Changed images to equations (McAdams, David E.)
3/25/2008: Changed More Information to current standard. (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License