Degree of an Equation

Pronunciation: /dɪˈgri/ Explain

The degree of an equation is the maximum number of times any variable or variables are multiplied together in any single term.^[1] The degree of an equation is used to help decide how to solve an equation, or whether or not an equation has a solution.

Form of an Equation

To determine the degree of an equation, first eliminate any parenthesis by using the distributive property of multiplication over addition and subtraction. Take the equation:

It may not be clear just by looking at that equation (1) has a degree of 2. To verify this, use the distributive property of multiplication over addition and subtraction to multiply it out: Now it is clear that both equations are of degree 2.

Terms of an Equation

When determining the degree of an equation, it is important to be able to recognize different terms. For more information on recognizing different terms see Term. The next equation shows an equation divided into terms:

Here is an example of an equation with two variables that is divided into terms:

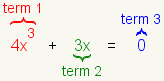
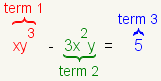
Degree of a Term

The degree of a single term is the sum of the exponents of any variables in the term. Start with the term 3x². The is only one variable in the term: x. The exponent of x is 2. So term 3x² has a degree of 2.

Now look at the term 14x. There is no exponent showing, so what is the degree? To figure this out, use the property of an exponent of 1: a¹ = a. The implied exponent of x is 1. So the term 14x has a degree of 1.

To find the degree of a term with more than one variable, add the exponents of each of the variables. The sum is the degree of the term. The degree of x²y⁴ is 2 + 4 = 6. The degree of the term g³h⁴k² is 3 + 4 + 2 = 9.

One more example. What is the degree of the term -3? Use another property of exponents: a⁰ = 1. Combine this with the property of multiplying by 1: 1·b = b. The term -3 can be written -3x⁰. The degree of this term then is 0. The degree of any constant term is 0.

Degree of an Equation

The degree of an equations is the largest degree of any term. In the equation

the degree of term 1 is 3. The degree of term 2 is 1. The degree of the constant term 3 is 0. The degree of the equation is the greatest of the degrees of the terms. This equation has degree 3.

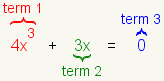
References

1. degree. merriam-webster.com. Encyclopedia Britannica. Merriam-Webster. Last Accessed 1/22/2010. http://www.merriam-webster.com/dictionary/degree.
2. Keigwin, H. W.. Principles of Elementary Algebra. pg 5. www.archive.org. Ginn & Company. 1886. Last Accessed 1/12/2010. http://www.archive.org/stream/principlesofelem00dupurich#page/5/mode/1up/search/degree. Buy the book
3. Bettinger, Alvin K. and Englund, John A.. Algebra and Trigonometry. pp 17-18. www.archive.org. International Textbook Company. January 1963. Last Accessed 1/12/2010. http://www.archive.org/stream/algebraandtrigon033520mbp#page/n34/mode/1up/search/degree. Buy the book

Cite this article as:

McAdams, David E. Degree of an Equation. 7/4/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/d/degree.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

7/4/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
1/22/2010: Added "References", expanded discussion of the degree of a term with more than one variable, and corrected typo in final paragraph on degree of an equation. (McAdams, David E.)
11/25/2008: Changed equations to images. (McAdams, David E.)
7/19/2008: Initial version. (McAdams, David E.)