Exact Values of Trigonometric Functions
Pronunciation: /ɪgˈzækt ˈvæl.juz ʌv ˌtrɪg.əˈnɒm.ɪ.trik ˈfʌŋk.ʃənz/ Explain| The exact values of trigonometric functions are values of trigonometric functions of certain angles that can be expressed exactly using expressions containing real numbers and roots of real numbers. These values are also called analytic values of trigonometric functions or trigonometric values of special angles. These angles are often used on tests where a calculator is not allowed, so it is useful for students to memorize these angles and the values of trigonometric functions of these angles. A mnemonic for remembering these values is at the end of this article. |
| |||||||||||||||||||||||||||||||||||||||||||||
Mnemonic What is this?
A mnemonic for remembering the values of sine for special angles is:
 |
| Figure 1: Mnemonic for sine of special angles |
A mnemonic for the cosine values of special angles is similar:
 |
| Figure 1: Mnemonic for cosine of special angles |
References
- McAdams, David E.. All Math Words Dictionary, exact values of trigonometric functions. 2nd Classroom edition 20150108-4799968. pg 74. Life is a Story Problem LLC. January 8, 2015. Buy the book
Cite this article as:
McAdams, David E. Exact Values of Trigonometric Functions. 12/21/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/e/exactvaltrig.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)7/5/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
2/1/2010: Added "References". (McAdams, David E.)
12/26/2009: Combined with Analytic Values of Trigonometric Functions and added reference. (McAdams, David E.)
1/7/2009: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License
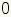
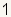
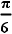 rad
rad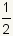
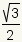
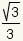
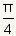 rad
rad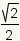
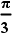 rad
rad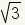
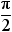 rad
rad
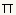 rad
rad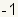
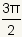 rad
rad