Fraction Rules
Pronunciation: /ˈfræk.ʃən rulz/ Explain
|
Fraction rules are a set of algebraic rules for working with fractions. A fraction has a numerator and a denominator. A fraction represents a division operation. The numerator is the dividend. The denominator is the divisor. |
| Operation | Equations | Examples | Description |
|---|---|---|---|
| Adding two fractions[2] | 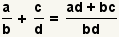 | 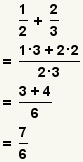 | To add fractions, transform each fraction so they have a common denominator. Add the numerators and use the common denominator as the denominator. Reduce the fraction. See Operations on Fractions: Addition and Subtraction. |
| Subtracting two fractions | 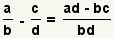 | 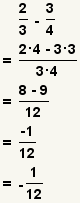 | To subtract fractions, transform each fraction so they have a common denominator. Subtract the numerators and use the common denominator as the denominator. Reduce the fraction. See Operations on Fractions: Addition and Subtraction. |
| Multiplying two fractions[2] | 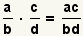 | 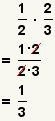 | To multiply fractions, multiply the numerators and multiply the denominators. Reduce the fraction. See Operations on Fractions: Multiplication. |
| Multiplying a fraction and a whole number. | 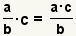 | 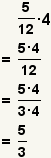 | To multiply a fraction and a whole number, multiply the numerator by the whole number. The denominator remains unchanged. Reduce the fraction if possible. |
| Dividing two fractions[2] | 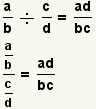 | 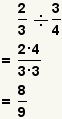 | To divide fractions, flip the divisor upside down then multiply by the dividend. Reduce the fraction. See Operations on Fractions: Division. |
| Dividing a fraction by an integer. | 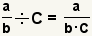 | 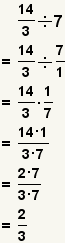 | To divide a fraction by a whole number, convert the whole number to a fraction, the divide the fractions.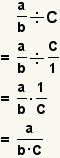 |
| Raising a fraction to a power. | 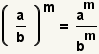 | 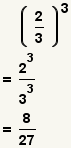 | See Operations on Fractions: Exponentiation. |
| Converting a mixed number to an improper fraction. | 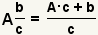 | 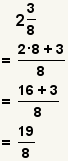 | To convert a mixed number to an improper fraction, multiply the whole part by the denominator and add the product to the numerator. The denominator remains unchanged. See How to Convert a Mixed Number to a Fraction. |
| Converting an improper fraction to a mixed number. | 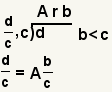 |  | To convert an improper fraction to a mixed number, divide the numerator by the denominator using a remainder. The mixed number is the quotient plus the remainder divided by the denominator. See How to Convert a Fraction to a Mixed Number.. |
| Zero numerator. | 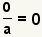 | 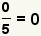 | Applying the property of multiplying by zero, a zero numerator with a zero denominator is zero. See Property of Multiplying by 0. |
| Zero denominator. |  |  | Since division by zero is undefined, a zero denominator makes the fraction undefined. |
| One minus sign. | 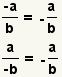 |  | Since 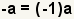 , apply the associative property of multiplication to get , apply the associative property of multiplication to get 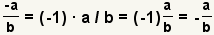 |
| Two minus signs. | 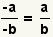 | 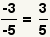 | Since 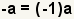 , apply the associative property of multiplication to get , apply the associative property of multiplication to get 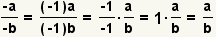 |
| If a fraction has the same nonzero numerator and denominator, the fraction's value is 1. | 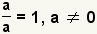 | 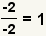 | Anything except 0 divided by itself is 1. |
| Any integer can be made into a fraction. | 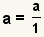 | 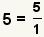 | Since 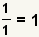 , apply the property of multiplying by 1: , apply the property of multiplying by 1: 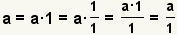 . See Property of Multiplying by 1. . See Property of Multiplying by 1. |
| Reducing fractions. | 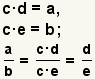 | 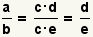 | Given two arbitrary values a and b, and values c, d, and e such that a = c · d and b = c · e, 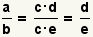 . See Reducing Fractions. . See Reducing Fractions. |
| Building fractions. | 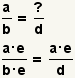 | 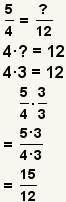 | Given a fraction a / b and a number d that is a multiple of d, find e such that b · e = d, then a / b = (a · e) / (b · e). |
| Operations on complex fractions. | Simplify the complex fractions, then use the rules for simple fractions. | 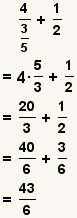 | To manipulate a complex fraction, convert it to a simple fraction, then follow the rules for simple fractions. See Complex Fraction. |
| Converting a decimal number to a fraction. | 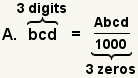 | 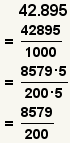 | To convert a decimal to a fraction, change the decimal to a whole number and divide it by 10n where n is the number of digits after the decimal point. |
| Converting a percentage to a fraction. | 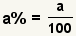 | 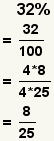 | To convert a percentage to a fraction, use the percentage as the numerator, 100 as the denominator, then simplify. |
| Comparing fractions with like denominators. | 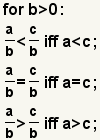 | 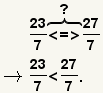 | To compare fractions with like denominators, compare the numerators. The relationship between the fractions is the same as the relationship between the denominators. |
| Comparing fractions with unlike denominators. | 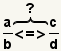 | 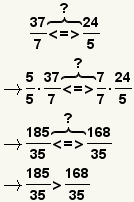 | To compare fractions with unlike denominators, either convert them to a decimal or transform them to a common denominator, then compare them. |
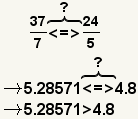 | |||
| Table 1 | |||
References
- McAdams, David E.. All Math Words Dictionary, fraction rules. 2nd Classroom edition 20150108-4799968. pg 82. Life is a Story Problem LLC. January 8, 2015. Buy the book
- Fine, Henry B., Ph. D.. Number-System of Algebra Treated Theoretically and Historically. 2nd edition. pp 12-15. www.archive.org. D. C. Heath & Co., Boston, U.S.A.. 1907. Last Accessed 7/11/2018. http://www.archive.org/stream/thenumbersystemo17920gut/17920-pdf#page/n21/mode/1up/search/fraction. Buy the book
- Oberg, Erik. Arithmetic Simplified. pp 21-31. www.archive.org. Industrial Press. 1914. Last Accessed 7/11/2018. http://www.archive.org/stream/arithmeticsimpli00oberrich#page/21/mode/1up/search/fraction. Buy the book
- Oberg, Erik. Elementary Algebra. pg 23. www.archive.org. Industrial Press. 1914. Last Accessed 7/11/2018. http://www.archive.org/stream/elementaryalgebr00oberrich#page/n26/mode/1up/search/fraction. Buy the book
- Bettinger, Alvin K. and Englund, John A.. Algebra and Trigonometry. pp 9-11,36-40. www.archive.org. International Textbook Company. January 1963. Last Accessed 7/11/2018. http://www.archive.org/stream/algebraandtrigon033520mbp#page/n18/mode/1up. Buy the book
More Information
- How to Multiply and Divide Fractions in Algebra (video). dummies.com. Wiley. 1/23/2010. http://www.dummies.com/how-to/content/how-to-multiply-and-divide-fractions-in-algebra.html.
Cite this article as:
McAdams, David E. Fraction Rules. 4/21/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/f/fractionrules.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/21/2019: Modified equations and expression to match the new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
8/28/2018: Corrected spelling. (McAdams, David E.)
7/9/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
2/5/2010: Added "References". (McAdams, David E.)
1/14/2009: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License
