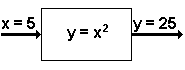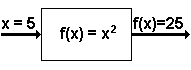Function

Pronunciation: /ˈfʌŋk.ʃən/ Explain

Figure 1: Function	A function can be considered like a box with an input and an output.[2] For each input that goes into the box, a single output comes out of the box. See figure 1. For any particular input that goes into the box, the same output always comes out of the box.
Figure 2: Function f(x)=x2	In figure 2, the function is labeled y = x2. 'y = x2' is the rule for transforming the input into the output. For any number input into the function, square the number to get the output. Note that every time the number 5 is input into the function, the number 25 is the output. The input of 5 will generate only the output of 25.
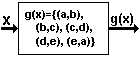
Figure 3: Function g(x)={(a,b), (b,c), (c,d), (d,e), (e,a)}	Functions are defined mathematically as a set of ordered pairs. The first value in the ordered pair is the input, and the second value is the output. The ordered pair for the function in figure 3 would be (5,25). 5 is the input and 25 is the output. For a function, the first value can not be repeated. Notice this allows exactly one output for each input. The definition of a function as a set of ordered pairs allows us to define functions that do not use numbers. Take the set {a, b, c, d, e}. If the function g(x) is defined as g(x) = {(a,b), (b,c), (c,d), (d,e), (e,a)}, one can tell what comes out of the function given what goes in. If a is the input, b is the output. For many functions, using an enumerated set of ordered pairs to define the function is not practical, since there are infinitely many inputs and outputs. A rule is typically used in these cases. A rule can define infinitely many ordered pairs without having to list each ordered pair.
Figure 4: Function Figure 5: Function	In the algebra of real numbers, functions are defined using variables. The input is called the independent variable. The output is called the dependent variable. A particular value of the independent variable, or input, generates exactly one value of the dependent variable. One example of an algebraic function is y = x2. x is independent variable. x can be any number which can be squared. So x is independent of anything else. y is the dependent variable. The value of y depends on the value of x. For example: If x = 5, y = 25. When x is 5, y can not be anything but 25. This is because the function states y = x2, so y must always be the square of x.

Function Notation

Figure 6: Function notation

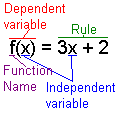
Function notation is commonly used way to write down functions. In the example in figure 6, x is the independent variable, f is the function name, f(x) is the dependent variable, and 3x + 2 is the rule for transforming x to f(x). See also Function Notation.

Domain and Range of Functions

Each function has a domain and a range. The domain is all the values that the independent variable can take. See Domain for more information. The range is all the values that the dependent variable can take. See Range for more information.

Representations of Functions

Functions can be represented in many ways. Table 1 shows the most common ways.

Representation	Description
{(1,3), (2,7), (4,-5)}	A set of ordered pairs where the first value is the input and the second value is the output.
f(n) where n is a positive integer and f(n) is the nth Fibonacci number.	A written description.
y = 3x + 2	An equation with an independent variable and a dependent variable
f(x) = x2	Function notation
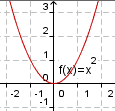	A graph where the horizontal axis represents the independent variable and the vertical axis represents the dependent variable.
x f(x) 1 4 2 7 3 -2 4 6	A table where one column or row represents the independent variable. Another column or row represents the dependent variable.
Table 1: Representations of functions

Operations on Functions

Functions that are defined over real numbers can be added, subtracted, multiplied and divided just like numbers. Also, functions can be composed.

Operation	Definition	Associativity	Commutativity
Addition	(f + g)(x) = f(x) + g(x)	(f + (g + h))(x) = ((f + g) + h)(x)	(f + g)(x) = (g + f)(x)
Subtraction	(f - g)(x) = f(x) - g(x)	(f - (g - h))(x) = ((f - g) - h)(x)	(f - g)(x) ≠ (g - f)(x)
Multiplication	(f · g)(x) = f(x) · g(x)	(f · (g · h))(x) = ((f · g) · h)(x)	(f · g)(x) = (g · f)(x)
Division	(f ÷ g)(x) = f(x) ÷ g(x)	(f ÷ (g ÷ h))(x) = ((f ÷ g) ÷ h)(x)	(f ÷ g)(x) ≠ (g ÷ f)(x)
Composition	(f ° g)(x) = f(g(x))	(f ° (g ° h))(x) = ((f ° g) ° h)(x)	(f ° g)(x) ≠ (g ° f)(x)
Table 2: Summary of operations on functions.

Addition and Subtraction of Functions

Addition of functions is defined as (f + g)(x) = f(x) + g(x). To add two functions, add all like terms from each function. Addition of functions of real numbers is associative: (f + (g + h))(x) = ((f + g) + h)(x). Addition of functions of real numbers is commutative: (f + g)(x) = (g + f)(x).

Step	Equations	Description
1		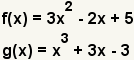These are the functions to add.
2		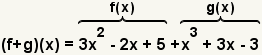Use the definition of function addition to create the new function.
3		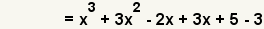Use the commutative property of addition to place the terms of the new function in order of degree.
4		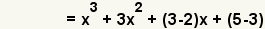Use the distributive property of multiplication over addition and subtraction to start to combine like terms.
5		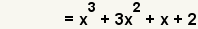Simplify the addition.
Table 3: Addition of functions

To subtract two functions, subtract all like terms from each function. The definition of function subtraction is (f - g)(x) = f(x) - g(x). Subtraction of functions is associative: (f - (g - h))(x) = ((f - g) - h)(x). Subtraction of functions is not commutative: (f - g)(x) ≠ (g - f)(x).

Step	Equations	Description
1		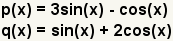These are the functions to subtract.
2		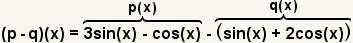Use the definition of function subtraction to form the new function.
3		Distribute negation over the second function.
4		Use the commutative property of addition to place the terms of the new function in order of degree.
5		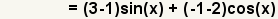Use the distributive property of multiplication over addition and subtraction to start to combine like terms.
6		Simplify the addition.
Table 4: Subtraction of functions

Multiplication of Functions

To multiply two functions, multiply each term of the first function by each term of the second function. Function multiplication is defined as (f · g)(x) = f(x) · g(x). Multiplication of functions of real numbers is associative: f(x) · (g(x) · h(x)) = (f(x) · g(x)) · h(x). Multiplication of functions of real numbers is commutative: f(x) · g(x) = g(x) · f(x).

Step	Equations	Description
1		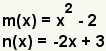These are the functions to multiply.
2		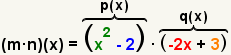Use the definition of function multiplication to form the new function.
3		Multiply each term from the first function times each term from the second function. Since both of these functions are binomials, use the FOIL method.
4		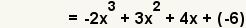Simplify the multiplication.
5		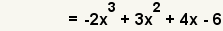Simplify the parentheses.
Table 5: Multiplication of functions

Division of Functions

To divide functions, create a fraction with the dividend in the numerator and the divisor in the denominator. Simplify the fraction, if possible. The definition of function division is: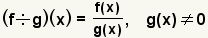 Division of functions of real numbers is associative: f(x)/(g(x) / h(x)) = (f(x) / g(x)) / h(x). Division of functions of real numbers is not commutative: f(x) / g(x) ≠ g(x) / f(x).

Step	Equations	Description
1		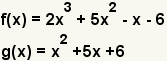These are the functions to divide.
2		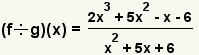Use the definition of function division to form the new function.
3		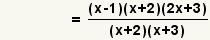Find common factors for the numerator and denominator.
4		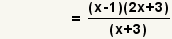Eliminate common factors.
5		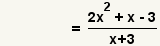Rewrite the function using polynomials in standard form.
Table 6: Division of functions

Composition of Functions

Composition of functions is taking the function of a function. For example, if f(x) = x² + 1, and g(x) = x - 2, then the composition of f(x) and g(x), written f°g(x) is f(g(x)) = (x - 2)² + 1 = (x² - 4x + 2) + 1 = x² - 4x + 3. Composition of functions of real numbers is associative: f°(g°h)(x) = (f°g)°h(x). Composition of functions of real numbers is not commutative: f°g(x) ≠ g°f(x).

Step	Equations	Description
1		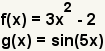These are the functions to compose.
2		Use the definition of composition to compose the two functions.
3		Simplify the expression.
2		Now find g°f. Use the definition of composition to compose the two functions.
3		Simplify using the distributive property of multiplication over addition and subtraction.
Table 7: Composition of functions

References

1. McAdams, David E.. All Math Words Dictionary, function. 2nd Classroom edition 20150108-4799968. pg 83. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. Fine, Henry B., Ph. D.. Number-System of Algebra Treated Theoretically and Historically. 2nd edition. pg 44. www.archive.org. D. C. Heath & Co., Boston, U.S.A.. 1907. Last Accessed 7/11/2018. http://www.archive.org/stream/thenumbersystemo17920gut/17920-pdf#page/n53/mode/1up/search/function. Buy the book
3. Goldrei, D.C.. Classic Set Theory: For Guided Independent Study. pp 4-5. Chapman & Hall Mathematics. July 1, 1996. Last Accessed 7/11/2018. Buy the book
4. Gilbert, Jimmie; and Gilbert Linda. Elements of Modern Algebra. 6th edition. pp 12-25. Thomson, Brooks/Cole. 2005. Last Accessed 7/11/2018. Buy the book

More Information

• McAdams, David E.. Domain. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 3/12/2009. https://www.allmathwords.org/en/d/domain.html.

Cite this article as:

McAdams, David E. Function. 4/21/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/f/function.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/21/2019: Modified equations and expression to match the new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/9/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
2/5/2010: Added "References". (McAdams, David E.)
3/10/2009: Clarified definition of function notation. (McAdams, David E.)
2/11/2009: Added section on operations on functions. (McAdams, David E.)
8/2/2008: Rewrote entire article. (McAdams, David E.)
8/20/2007: Add this revision history. (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)