Hexagon

Pronunciation: /ˈhɛk.səˌgɒn/ Explain

An image showing various hexagons. All of the hexagons have six straight sides. Some are concave, and some are convex. Two of the hexagons are convex, equilateral hexagons, which ar regular hexagons.
Figure 1: hexagons.

A hexagon is a six sided polygon. The sides of a hexagon are straight line segments. A hexagon is a planar figure, a figure that exists in a plane. A hexagon can be concave or convex. If a convex hexagon is equilateral (the sides are the same length), then the hexagon is a regular hexagon.

Article Index

Hexagon
Regular Hexagon
Parts of a Regular Hexagon
Formulas for a Regular Hexagon
How to Construct a Regular Hexagon From its Circumcircle
How to Construct the Center, Incircle and Circumcircle of a Regular Hexagon
Tessellations of a Regular Hexagon
Natural and Manufactured Hexagons

Regular hexagon

A regular hexagon is a six sided, equilateral, convex polygon. An equilateral polygon has sides that are all the same length. No line segment drawn between any two points in a convex figure leaves the figure.

Click on the blue points and drag them to change the figure.

When is the length of a side different from the length of the circumradius?
Manipulative 1 - Regular Hexagon Created with GeoGebra.

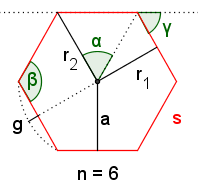
Parts of a regular hexagon

  • side or edge: One of the line segment that makes up hexagon. The length of a side of a regular hexagon will be denoted s in this article.
  • vertex: Where two of the sides of the hexagon meet.
  • interior: The area inside the hexagon.
  • exterior: The area outside the hexagon.
  • boundary: The sides and vertices of the hexagon.
  • center: The point at the middle of the hexagon. The center of a regular hexagon can be found at the intersection of the perpendicular bisectors of any two sides. See How to Construct the Center, Incircle and Circumcircle of a Regular Hexagon. The center of a regular hexagon is also its centroid.
  • incircle: A circle whose center is at the center of a regular hexagon that touches each side of the hexagon once. In this article, the radius of the incircle will be denoted r1.
  • circumcircle: A circle whose center is at the center of a regular hexagon that intersects each of the vertices of the regular hexagon. In this article, the radius of the circumcircle will be denoted r2.
  • apothem: A line segment from the center of a regular hexagon to the midpoint of one of the sides. The length of the apothem is the same as the radius of the incircle and is denoted (r1).
  • sagitta: A line segment from the center of a side to the edge of the circumcircle of a regular hexagon that is collinear with the apothem.
  • central angle:: The angle between two line segments extending from the center of the regular hexagon to two adjacent vertices. The central angle of a regular hexagon is always 72°.
  • interior angle: The angle between two adjacent sides. The interior angles of a regular hexagon always measure 120°. The sum of the measures of interior angles of any convex hexagon is 720°.
  • exterior angle: The angle between the extended side of a regular hexagon and an adjacent side. The exterior angles of a regular hexagon always measure 60°.

Formulas for a regular hexagon

IllustrationFormulaDescription
A hexagon with a side labeled 's', a line segment from the center to a vertex labeled 'r1', a line segment from the center to the midpoint of a side labeled 'r2' and 'a', a line segment from the midpoint of a side to the edge of the circumcircle labeled 'g', an angle between two line segments from the center to adjacent vertices labeled 'alpha', the angle at a vertex on the inside of the hexagon labeled 'beta', and the angle on the outside of the hexagon between and extended side and an adjacent side labeled 'gamma'. n = 6number of sides
slength of a side
p = 6sperimeter
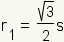r1=square root(3)/2*sradius of the incircle
r2 = sradius of the circumcircle
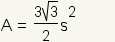A=((3*square root(3))/2)*s^2.area of the hexagon
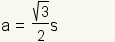a=((square root(3))/2)*s.length of the apothem
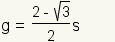g=((2-square root(3))/2)*s.length of the sagitta
α = 72°measure of the central angles
β = 120°measure of the interior angles
γ = 60°measure of the exterior angles
Table 1: Formulas for a regular hexagon.

How to Construct a Regular Hexagon from its Circumcircle

StepIllustrationDescription and Justification
1 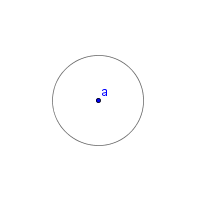A circle with a center point. The center of the circle is labeled a. Draw a circle. Label the center of the circle a. This is given.
2 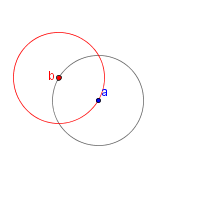A circle with a center point that is labeled a. An circle with the same radius as a is draw with a center point on the circumference of circle a. This circle intersects circle a twice. The center of the second circle is labeled b. Draw a circle with the center on the circumference of circle a that is the same radius as circle a. Label the center of this circle b.
3 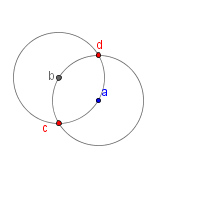A circle with a center point that is labeled a. Another circle labeled b with its center on the edge of circle a that has the same radius as circle a. The two intersections of the circles are labeled c and d. Label the intersections of the circles c and d.
4 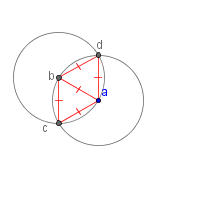Circles a and b and intersections c and d with line segments ab, ac, ad, bc and bd drawn in. Draw line segments ab, ac, ad, bc and bd. Note that all of these line segments are radii of congruent circles. This means that they are all the same length. So triangles Δabc and Δabd are equilateral triangles, triangles whose sides have the same measure. The angles of equilateral triangles also have the same measure. Therefore, triangles Δabc and Δabd are congruent by the SAS Congruence Theorem.
5 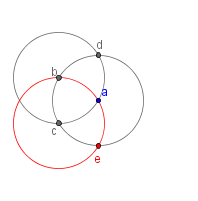Circles a and b with a circle drawn with center point at c and the same radius as a and b. The intersection of the circle centered at c and circle a is labeled e. Draw another circle with the same radius as a with a center at c. Label the new intersection of circle c and circle a as e.
6 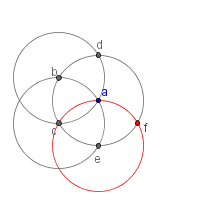Circles a, b and c. Another circle is drawn with center at <var>e</var> that has the same radius as circle a. Draw another circle with the same radius as a with a center at e. Label the new intersection of circle e and circle a as f. Note that by the same arguments that were used in step 5, triangles Δabc and Δace are congruent equilateral triangles.
7 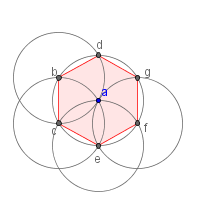Circle a with circles b, c, d, e, f and g drawn with centers on a. Continue the pattern until circles with centers at b, c, d, e, f and g are drawn. We know this is a regular hexagon because
  1. There are six sides. Count them.
  2. Each of the sides is a straight line segment. They were drawn as a straight line segment.
  3. The sides are all the same size. See the reasoning in step 4.
  4. The figure is a convex.
Items 1 and 2 match the definition of a hexagon, so the figure must be a hexagon. Items 1 through 4 match the definition of a regular hexagon, so the figure must be a regular hexagon.
Table 2: How to construct a regular hexagon from its circumcircle.

How to Construct the Center, Incircle and Circumcircle of a Regular Hexagon

StepIllustrationDiscussion and Justification
1 A regular hexagon The center of a regular hexagon is at the point of concurrency of perpendicular bisectors of any two sides that are not opposite each other.
2 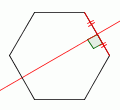A regular hexagon with the perpendicular bisector of one of the sides drawn in. Draw the perpendicular bisector of any side.
3 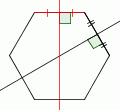A regular hexagon with the perpendicular bisector of two of the non-opposite sides drawn in. Draw the perpendicular bisector of any other side that is not opposite the side you used in step 2.
4 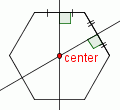A regular hexagon with the perpendicular bisector of two of the non-opposite sides drawn in. The intersection of the two perpendicular bisectors in labeled 'center'. Label the intersection of the two perpendicular bisectors as 'center'.
5 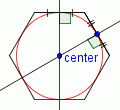A regular hexagon with the perpendicular bisector of two of the non-opposite sides drawn in. The intersection of the two perpendicular bisectors in labeled 'center'. A circle is drawn with the center at 'center' and the edge at the midpoint of one of the sides. Draw a circle with a center at the point labeled 'center' and the edge at a point where a perpendicular bisector intersects a side. This is the incircle.
6 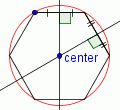A regular hexagon with the perpendicular bisector of two of the non-opposite sides drawn in. The intersection of the two perpendicular bisectors in labeled 'center'. A circle is drawn with the center at 'center' and the edge at any vertex. Draw a circle with a center at the point labeled 'center' and the edge at any vertex. This is the circumcircle.
Table 3 - How to construct the center, incircle and circumcircle of a regular hexagon

Tessellations of a Hexagon

A tessellation of one or more polygon is an arrangement of those polygons that fills a plane. The are a number of tessellations that use hexagons. Most of the tessellations shown here use regular hexagons.

A regular tessellation of hexagons. Around each vertex are three identical hexagons. Hexagon tessellation 2
A regular tessellation of a hexagon. Three hexagons are around each vertex. A trihexagonal tiling. Each vertex has a regular hexagon, an equilateral triangle, a regular hexagon and an equilateral triangle.
Table 4: tessellations of a hexagon

Natural and Manufactured Hexagons

Hexagonal pavement tiles. Hexagonal cloud formation on the north pole of Saturn. An array of hexagonal mirrors with a man measuring the mirrors.
A hexagonal pavement. Hexagonal cloud formation on Saturn. A hexagonal mirror array.
A diagram of carbon 36 fullerene molecules showing the hexagonal structure. Hexagonal basalt formation polished by a glacier. A hexagonal honeycomb with bees on it.
Carbon 36 fullerene molecules. Hexagonal basalt formation polished by a glacier. A hexagonal honeycomb.
Table 5: Natural and Manufactured hexagons. Click on each image for more information on the image.

References

  1. McAdams, David E.. All Math Words Dictionary, hexagon. 2nd Classroom edition 20150108-4799968. pg 90. Life is a Story Problem LLC. January 8, 2015. Buy the book

More Information

  • McAdams, David E.. Polygon. allmathwords.org. Life is a Story Problem LLC. 10/22/2010.

Cite this article as:

 McAdams, David E. Hexagon. 4/22/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/h/hexagon.html.

Image Credits

Revision History

4/22/2019: Update equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/16/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
10/22/2010: Initial version. (McAdams, David E.)

All Math Words Encyclopedia is a service of Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License