Radical
Pronunciation: /ˈræd.ɪ.kəl/ ExplainA radical is a root of a number or
expression, such as 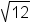 .
Definition:
.
Definition: 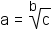 if and only if
if and only if 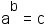 .
The word radical can also be used to indicate the symbol indicating root,
such as
.
The word radical can also be used to indicate the symbol indicating root,
such as 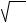 .
When used as an adjective, the word radical means 'having to do with
the taking of a root'. For example, a
radical equation is an equation containing
a variable inside a radical, or the root of a variable.
.
When used as an adjective, the word radical means 'having to do with
the taking of a root'. For example, a
radical equation is an equation containing
a variable inside a radical, or the root of a variable.
A radical with no number to the left is used to represent a square
root. For example, 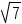 means the
square root of 7. If an integer appears to the left of the radical
sign, it means an nth root. The expression
means the
square root of 7. If an integer appears to the left of the radical
sign, it means an nth root. The expression
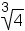 means the cube root of 4. The expression
means the cube root of 4. The expression 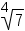 means the 4th root of 7.
means the 4th root of 7.
A radicand is the number or expression inside a radical:
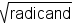 . For example:
in
. For example:
in 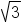 , 3 is the
radicand; in
, 3 is the
radicand; in 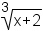 ,
x + 2 is the radicand; and in
,
x + 2 is the radicand; and in 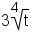 ,
t is the radicand.
,
t is the radicand.
Radicals and exponentiation
|
A radical is the same as a exponent of a unit fraction. For example,
|
|
How to Simplify a Radical
A radical can be simplified if it contains a factor raised to the power of
the radical. For example, Since
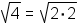 ,
and
,
and 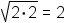 ,
then
,
then 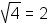 .
The steps to simplifya radical are:
.
The steps to simplifya radical are:
- Find the prime factorization of the radicand. A factor tree is useful here.
- Divide into groups of factors with the same value. The size of each group is the number to the left of the radical or, if there is no number to the left of the radical, the size of the groups is 2.
- Bring out the groups of factors. For each group brought out, there
is an exponent of 1. For example, in
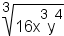 , bring
out factors in in groups of 3:
, bring
out factors in in groups of 3:
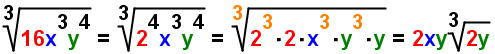 .
.
| Equation to simplify | Prime factorization | Divided into groups | Groups pulled out |
|---|---|---|---|
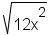 |
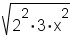 |
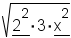 |
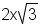 |
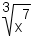 |
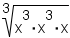 |
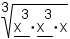 |
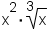 |
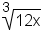 |
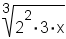 |
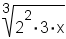 . Note that there are no groups
of 3. . Note that there are no groups
of 3. |
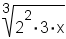 . This radical can not be
simplified. . This radical can not be
simplified. |
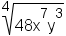 |
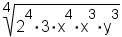 |
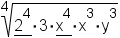 |
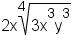 |
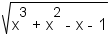 |
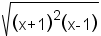 |
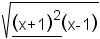 |
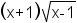 |
| Table 2: Examples of simplifying radicals | |||
Common phrases using radical
- radical expression: An expression containing a variable in a radical, such as
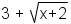 . Note that an expression with a
number inside a radical, but no variable, is not a radical expression.
. Note that an expression with a
number inside a radical, but no variable, is not a radical expression.
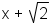 is not a radical expression.
is not a radical expression. - radical equation: An equation containing a variable in a radical, such as
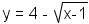 . Note that an equation with a
number inside a radical, but no variable, is not a radical equation.
. Note that an equation with a
number inside a radical, but no variable, is not a radical equation.
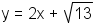 is not a radical equation.
is not a radical equation. - radical function: A function containing a variable in a radical, such as
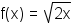 . Note that a function with a
number inside a radical, but no variable, is not a radical function.
. Note that a function with a
number inside a radical, but no variable, is not a radical function.
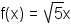 is not a radical function.
is not a radical function.
References
- McAdams, David E.. All Math Words Dictionary, radical. 2nd Classroom edition 20150108-4799968. pg 149. Life is a Story Problem LLC. January 8, 2015. Buy the book
Cite this article as:
McAdams, David E. Radical. 5/3/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/r/radical.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
5/3/2019: Changed equations and expressions to new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/4/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
12/6/2010: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License
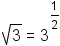 . In general,
. In general,
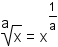 . To convert
a radical to an exponent, make the radicand the base, and the number to
the left of the radical the denominator of the unit fraction in the exponent.
. To convert
a radical to an exponent, make the radicand the base, and the number to
the left of the radical the denominator of the unit fraction in the exponent.
