Real Number
Pronunciation: /ˈriəl ˈnʌm.bər/ ExplainA real number is a number that can be found on the real number line. At first, this may seem a silly way to define a real number. But, when you look into it, you can see why this makes sense.
First off, any whole number or integer is a real number. Usually, we use whole number for our tick-marks on the real number line as in figure 1:

Figure 1: Number line from -3 to 3. |
Obviously, we can find any integer on the number line simply by extending the number line far enough. How about rational numbers? Take 1/2 for instance. It can be found halfway between zero and one as shown in figure 2.

Figure 2: Number line with the number 1/2 marked. |
Now look at irrational numbers. Take 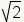 for instance. The value of
for instance. The value of 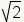 is about 1.41. So it is on the number line. See figure 3
for this example.
is about 1.41. So it is on the number line. See figure 3
for this example.

Figure 3: Number line with 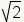 marked. marked. |
And how about the number for π? Yes! It's right there between 3 and 4 as shown in figure 4.

Figure 4: Number line with π marked. |
So what numbers are not on the real number line? The answer is
complex numbers.
The diagram below is the complex number plane.
Real numbers can be found on the real number line which is the horizontal axis. Any
other complex number is found on the complex plane, but not on the real number line.
There are three numbers labeled on the plane in figure 5. The first is
A( 2, 0 ). Since this is on the real number
line it is a real number. The second is B( 0, √2
). This is the number 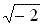 .
It is not on the real number line. The third is
C(1,1). This is
the number 1 + i. It, too, is not on the real number line.
So
.
It is not on the real number line. The third is
C(1,1). This is
the number 1 + i. It, too, is not on the real number line.
So 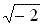 and 1 + i are not real numbers.
and 1 + i are not real numbers.
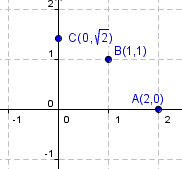
Figure 5: The complex plane. |
Types of Real Numbers
The set of real numbers can be divided into several subsets:
| Subset name | Description | Examples |
|---|---|---|
| Natural numbers | A natural number is a positive whole number: ℕ = {1, 2, 3, 4, …}. | 1, 17, 2, 325, 985 |
| Integers | An integer is a positive or negative whole number: ℤ = {…, -3, -2, -1, 0, 1, 2, 3, …}. | -3, 19, 215 |
| Rational numbers | Any number that can be expressed as the ratio of two integers. {x = a / b | a, b ∈ ℤ}. | 3 = 1/3, -6/5, 22/7 |
| Irrational numbers | Any real number that is not a rational number. | π, 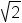 |
| Algebraic number | Any number that is a root of a single variable, nonzero polynomial with rational coefficients. | 5, -3/2, 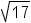 , , 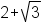 . . |
| Transcendental number | Any real number that is not an algebraic number. | π, e. |
| Table 1: Types of real numbers. | ||
Properties of Real Numbers
| Property | Description |
|---|---|
| Associativity | The set of real numbers is associative with respect to addition, subtraction, multiplication and division. Example: a + (b + c) = (a + b) + c. |
| Commutativity | The set of real numbers is commutative with respect to addition and multiplication. The set of real numbers is not commutative with respect to subtraction or division. Example: a + b = b + a. |
| Additive identity | The additive identity for real numbers is 0. Example: a + 0 = 0 + a = a. |
| Multiplicative identity | The multiplicative identity for real numbers is 1. Example: a · 1 = 1 · a = a. |
| Closure | The set of real numbers is closed with respect to addition, subtraction, multiplication, and division. Example: if a and b are real numbers then a + b is also a real number. |
| Discrete | The set of real numbers is a continuous (not discrete) set. |
| Cardinality | The cardinality of the set of real numbers is ℵ0. |
| Trichotomy | The Trichotomy Property of Real Numbers states that for any two real numbers a and b, exactly one of the following is true: a < b, a = b or a > b. |
| Table 2: Properties of the real numbers. | |
Postulates and Theorems about Real Numbers
- Ruler postulate
The ruler posultate states that:- Every point on a line can be paired with a real number.
- The number associated with a point A on the line is called the coordinate of A.
- Two arbitrary points can be paired with the numbers 0 and 1, defining the length of a unit.
- The distance between any two points A and B is designated AB.
- The distance between two points is taken to be positive. Note that a directed distance can be positive or negative.
- The distance between two points A and B can be found by taking the absolute value of the difference of their coordinates.
- The set of real numbers does not have a one-to-one correspondence with the natural numbers. See Cardinality.
References
- McAdams, David E.. All Math Words Dictionary, real number. 2nd Classroom edition 20150108-4799968. pg 151. Life is a Story Problem LLC. January 8, 2015. Buy the book
Cite this article as:
McAdams, David E. Real Number. 5/3/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/r/realnumber.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
5/3/2019: Changed equations and expressions to new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/5/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
8/28/2018: Corrected spelling. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
5/5/2011: Added trichotomy property and postulate and theorems of real numbers, ruler postulate and the set of real numbers does not have a one to one correspondence with the set of natural numbers. (McAdams, David E.)
4/28/2011: Added Types of Real Numbers and Properties of Real Numbers. (McAdams, David E.)
12/31/2008: Added 'More Information'. (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License