Derivation of the Cofunction Trigonometric Identities
Pronunciation: /ˌdɛɹ.ɪˈveɪ.ʃən ʌv ðə koʊˈfʌŋk.ʃən ˌtrɪɡ.ə.nəˈmɛ.trɪk aɪˈdɛn.tə.tiz/ Explain| Step | Image | Equation | Discussion |
|---|---|---|---|
| 1 | 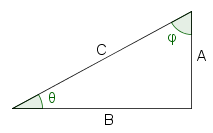 |
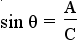 and and 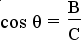 . . |
This is the definition of sine and cosine using the angle θ. |
| 2 |  |
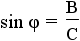 and and 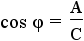 . . |
This is the definition of sine and cosine using the angle θ. |
| 3 |  |
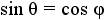 and and 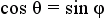 . . |
This is the definition of sine and cosine using the angle φ. |
| 4 |  |
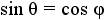 and and 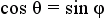 |
Apply the transitive property of equality to equate sin θ with cos φ and cos θ with sin φ. |
| 5 |  |
α + β + γ = &pi | This is the Angle Sum Theorem. |
| 6 |  |
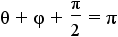 |
Use the subsitution property of equality to substitute θ for α, φ for β and 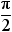 for γ. for γ. |
| 7 |  |
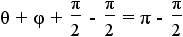 |
Apply additive property of equality to add -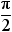 to both sides of the equation. to both sides of the equation. |
| 8 |  |
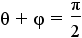 |
Simplify the equation by combining the constants on both sides of the equation. |
| 9 |  |
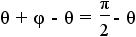 |
Apply the addition property of equality to add -θ to both sides of the equation. |
| 10 |  |
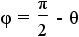 |
Cancel θ - θ on the left side of the equation. |
| 11 |  |
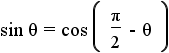 and and 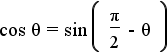 |
Take the equations from step 4 and apply the subsitution property of equality witht the equations from step 10. These are the first two cofunction identities. |
| 12 |  |
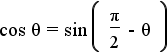 |
Use the equations from step 11, and the defintions of tangent and cotangent to get the tangent identity. |
| 13 |  |
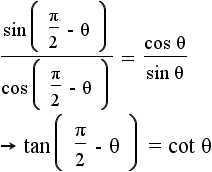 |
Use the equations from step 11, and the defintions of tangent and cotangent to get the cotangent identity. |
| 14 |  |
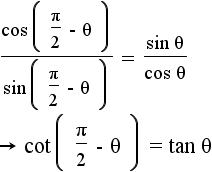 |
Use the equations from step 11, and the defintions of tangent and cotangent to get the cosecant identity. |
| 15 |  |
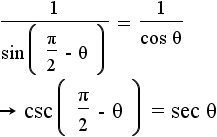 |
Use the equations from step 11, and the defintions of tangent and cotangent to get the secant identity. |
References
- McAdams, David E.. All Math Words Dictionary, derivation. 2nd Classroom edition 20150108-4799968. pg 58. Life is a Story Problem LLC. January 8, 2015. Buy the book
Cite this article as:
McAdams, David E. Derivation of the Cofunction Trigonometric Identities. 12/21/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/t/ti_cofunction.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)7/4/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
4/29/2011: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License