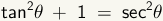Derivation of the Pythagorean Trigonometric Identities
Pronunciation: /ˌdɛɹ.ɪˈveɪ.ʃən ʌv ðə pɪˌθæ.gəˈri.ən ˌtrɪɡ.ə.nəˈmɛ.trɪk aɪˈdɛn.tə.tiz/ Explain| Image | Equation | Discussion |
|---|---|---|
 |
A2 + B2 = C2 | This is the equation given by the Pythagorean Theorem. |
 |
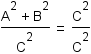 |
Use the multiplicative property of equality to multiply both sides by 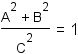 . . |
 |
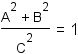 |
Since anything except zero divided by itself is one, substitute 1 for 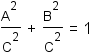 . . |
 |
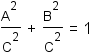 |
Use the distributive property of multiplication over addition and subtraction to distribute 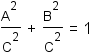 through the parentheses on the left side of the equation. through the parentheses on the left side of the equation. |
 |
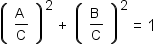 |
Apply the distributive property of exponentiation over division. |
 |
 |
The definition of sine is 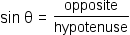 . The definition of cosine is . The definition of cosine is 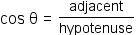 . Given angle θ, . Given angle θ, 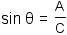 and and 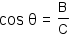 . Apply the substitution property of equality to substitute sin θ for . Apply the substitution property of equality to substitute sin θ for  and cos θ for and cos θ for  . . |
| Image | Equation | Discussion |
|---|---|---|
 |
 |
Start with the first Pythagorean identity. |
 |
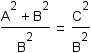 |
Apply the multiplication property of equality to the equation by multiplying both sides of the equation by 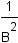 . . |
 |
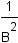 |
Apply the distributive property of multiplication over addition and subtraction. |
 |
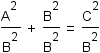 |
Since anything except zero divided by itself is one, substitute 1 for 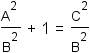 . . |
 |
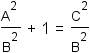 |
Since 12 = 1, apply the substiution property of equality to subtitute 12 = 1 for 1. |
 |
 |
Apply the distributive property of exponentiation over division to both sides of the equation. |
 |
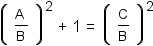 |
Use the definition of tangent to subsitute tan θ for 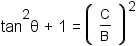 . . |
 |
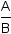 |
Use the definition of secant to subsitute sec θ for 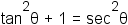 . . |
| Image | Equation | Discussion |
|---|---|---|
 |
 |
Start with the first Pythagorean identity. |
 |
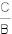 |
Apply the multiplication property of equality to the equation by multiplying both sides of the equation by 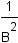 . . |
 |
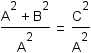 |
Apply the distributive property of multiplication over addition and subtraction. |
 |
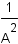 |
Since anything except zero divided by itself is one, substitute 1 for 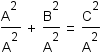 . . |
 |
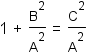 |
Apply the commutative property of addition. |
 |
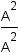 |
Since 12 = 1, apply the substiution property of equality to subtitute 12 = 1 for 1. |
 |
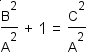 |
Apply the distributive property of exponentiation over division to both sides of the equation. |
 |
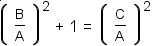 |
Use the definition of tangent to subsitute cot θ for 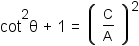 . . |
 |
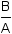 |
Use the definition of secant to subsitute csc θ for 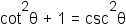 . . |
References
- McAdams, David E.. All Math Words Dictionary, derivation. 2nd Classroom edition 20150108-4799968. pg 58. Life is a Story Problem LLC. January 8, 2015. Buy the book
Cite this article as:
McAdams, David E. Derivation of the Pythagorean Trigonometric Identities. 12/21/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/t/ti_pythagorean.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)7/4/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
4/29/2011: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License