Diagrama de la caja y de los bigotes: Una manera de representar los datos gráficamente que demuestran la distribución de los datos.

Diagrama de la caja y de los bigotes

Se utiliza un diagrama de la caja y de los bigotes de demostrar la distribución de un conjunto de datos. Cada cuartila se marca en el gráfico, y una caja se dibuja para representar las 2das y 3ro cuartilas. Las rectas se dibujan para representar las 1ras y 4tas cuartilas. Éstas son los “bigotes�. El diagrama de la caja y de le bigote en el cuadro 1 representa el conjunto de datos {2, 2, 3, 4, 5, 5, 6, 7, 8, 9}.

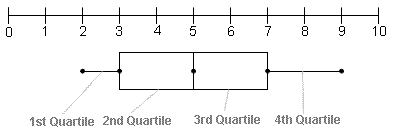Diagrama de la caja y de los bigotes
Cuadro 1: Diagrama de la caja y de los bigotes

Cómo dibujar un diagrama de la caja y de la barba

Por este ejemplo, utilice el conjunto de datos {1, 8, 4, 3, 9, 3, 6, 4, 7}.

PasoDescripciónEjemplo
1 Dibuje una Recta numérica que contenga el conjunto de datos. 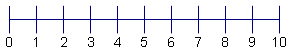Recta numérica a partir de la 0 a 10.
2 Determine el punto medio del conjunto de datos. El punto medio de este conjunto de datos es el drenaje 4 recta vertical debajo de los 4. 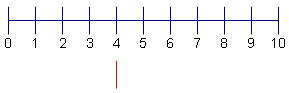Recta numérica a partir de la 0 a 10 con una recta marca 4.
3 Ahora calcule el comienzo de la 1ra cuartila. Tome la primera mitad del conjunto de datos: {1, 3, 3, 4}. Encuentre el punto medio de la primera mitad del conjunto de datos. En este caso, el punto medio es 3 + 3 = 6. 6/2 = 3. Haga una recta debajo de los 3. 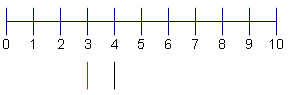Recta numérica a partir de la 0 a 10 con una recta bajo números 3-4.
4 Termine la caja para la 2da cuartila. 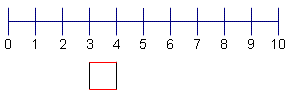Recta numérica a partir de la 0 a 10 con una caja de debajo 3-4 que demuestra la 2da cuartila.
5 Calcule el comienzo de la 4ta cuartila. Tome la segunda mitad del conjunto de datos: {6, 7, 8, 9}. Encuentre el punto medio de la segunda mitad del conjunto de datos. En este caso, el punto medio es 7 + 8 = 15. 15/2 = 7.5. Haga una recta debajo de 7.5. 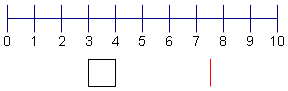Recta numérica a partir de la 0 a 10 con una recta bajo números 3-4.
6 Termine la caja para la 3ro cuartila. 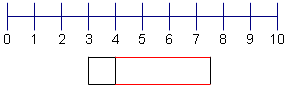Recta numérica a partir de la 0 a 10 con una caja de debajo 3-4 que demuestra la 2da cuartila y una caja debajo de 4-7.5 que demuestran la 3ro cuartila.
7 Ahora dibuje un punto para demostrar el comienzo de la 1ra cuartila. No incluya ninguna afloramientos. 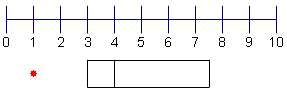Recta numérica a partir de la 0 a 10 con una caja de debajo 3-4 que demuestra la 2da cuartila y una caja debajo de 4-7.5 que demuestran la 3ro cuartila, y un punto debajo de 1 que marca el comienzo de la 1ra cuartila.
8 Conecte el punto con el centro de la 2da recta de la cuartila. Recta numérica a partir de la 0 a 10 con una caja de debajo 3-4 que demuestra la 2da cuartila y una caja debajo de 4-7.5 que demuestran la 3ro cuartila, y una recta a partir de la 1-3 que demuestra la primera cuartila.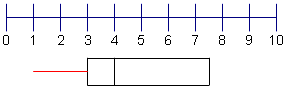
9 Ahora dibuje un punto para demostrar el final de la 4ta cuartila. No incluya ninguna afloramientos. 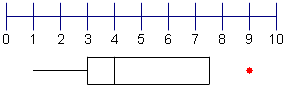Recta numérica a partir de la 0 a 10 con una caja de debajo 3-4 que demuestra la 2da cuartila y una caja debajo de 4-7.5 que demuestran la 3ro cuartila, y una recta a partir de la 1-3 que demuestra la primera cuartila, y un punto debajo de 9 que demuestran el final de la 4ta cuartila.
10 Conecte el punto con el centro de la 3ro recta de la cuartila. Su diagrama de la caja y de la barba es completo ahora. 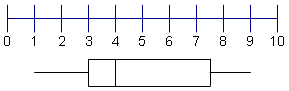Recta numérica a partir de la 0 a 10 con una caja de debajo 3-4 que demuestra la 2da cuartila y una caja debajo de 4-7.5 que demuestran la 3ro cuartila, y una recta a partir de la 1-3 que demuestra la primera cuartila, y una recta a partir del 7.5-9 que demuestran la 4ta cuartila.

Más información

Citar este artículo como:
Diagrama de la caja y de los bigotes. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/b/boxandwhiskerplot.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-06-07: Deletreo corregido (McAdams, David.)
2008-03-18: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License