Complemente (conjunto): Dado un conjunto S y un subconjunto A de S, el complemento de A es un conjunto de todos los miembros de S que no sean miembros del A.

Complemente (conjunto)

Conjunto universal

Una caja con un S. etiquetado interior amarillo.
Cuadro 1: Un conjunto universal S.

El concepto de comienzo del complemento con un conjunto universal. Un conjunto universal es un conjunto que contiene todos los elementos uno desea incluir. Si uno se está ocupando de números, el conjunto universal pudo ser todos los números reales, o todos los números enteros. Otras posibilidades del conjunto universal son todos los animales, o todos los estudiantes en una clase. Un conjunto universal es representado generalmente por una caja. Véase el cuadro 1.

Complemento de un conjunto

Una caja con un interior amarillo. La caja se etiqueta S. Un circunferencia está en la caja. El circunferencia tiene un interior azul y se etiqueta A.
Cuadro 2: Complemento de A en S: A \ S o A'.

El complemento de un conjunto es todos los elementos del conjunto universal que no son elementos del conjunto. En el cuadro 2, el conjunto universal es S. El conjunto A es representado por el interior azul del circunferencia. El complemento de A es la parte azul de S que no esté dentro del circunferencia A. Para escribir un complemento, escriba A \ S o A'. Para hablar de un complemento diga, “el complemento de A en S,� o “el complemento de A�.

Ejemplos

Deje el conjunto universal S ser el conjunto de todos los números enteros. Deje A ser el conjunto de todos los incluso números enteros. El complemento de A en S es todos los números enteros que no son números pares. Esto significa que el complemento de A es todos los números impares. Esto se puede escribir matemáticamente como: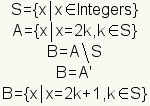

\ comienzan {arsenal} {c} S= \ {x \ mediados de {} x \ en {} \ mbox {} \} de los números enteros \ \ A= \ {x \ mediados de {} x=2k, k \ en {} S \} \ \ B=A \ setminus {} S \ \ B=A'\ \ B= \ {x \ mediados de {} x=2k+1, k \ en {} S \} \ extremo {arsenal}

Deje S ser el conjunto de todos los estudiantes en una sala de clase. Deje A ser el conjunto de todos los estudiantes femeninos en la sala de clase. Deje B ser el conjunto de todos los estudiantes masculinos en la sala de clase. Puesto que cada estudiante es varón o hembra, A=B'.

Conjuntos no-complementario

Una caja con un interior amarillo. La caja se etiqueta S. Dos circunferencias están en la caja. Un circunferencia tiene un interior azul y se etiqueta A. El otro circunferencia tiene un interior verde y se etiqueta B.
Cuadro 3: Conjuntos no complementarios.

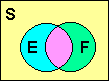
Dos conjuntos no son complementarios si los dos conjuntos juntos no incluyen el conjunto universal entero. En el cuadro 3, fije S es el conjunto universal. Hay del conjunto S que no están en el conjunto C o el conjunto D. D no está tan el complemento de C. indicado matemáticamente: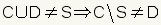

La unión D de C no iguala el setminus S de S->C no iguala D

Ejemplos

Deje S ser el conjunto de todos los animales. Deje C ser el conjunto de todos los gatos. Deje D ser el conjunto de todos los perros. Puesto que hay los animales que son ni perros ni gatos, C no es el complemento de D en el S.

Deje S ser el conjunto de toda la fruta. Deje C ser el conjunto de todas las manzanas. Deje D ser el conjunto de todas las naranjas. Puesto que hay fruta que es ni manzanas ni naranjas, C no es el complemento de D.

Una caja con un interior amarillo. La caja se etiqueta S. Dos circunferencias traslapados están en la caja. Un circunferencia tiene un interior azul y se etiqueta A. El otro circunferencia tiene un interior verde y se etiqueta B. La parte traslapada de los circunferencias A y B es púrpura.
Cuadro 4: Conjuntos no complementarios.

Los conjuntos no son también complementarios si se traslapan; si contienen a algunos de los mismos miembros (E∩F≠∅). En el cuadro 4, fija E y F contiene a algunos miembros comunes. Indicado matemáticamente: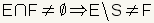

la intersección F de e no iguala el conjunto vacío - > el setminus S de E no iguala F

Ejemplo

Deje S ser el conjunto de todos los estudiantes en una escuela. Deje E ser todos los estudiantes con el pelo marrón. Deje F ser todos los estudiantes masculinos. Puesto que algunos estudiantes masculinos también tienen pelo marrón, los conjuntos se traslapan. F no es tan el complemento de E.

Definición formal

Una caja con un interior amarillo. La caja se etiqueta S. Un circunferencia está en la caja. El circunferencia tiene un interior azul y se etiqueta A.
Cuadro 5: Complemento de A en S

Dado un conjunto S y un subconjunto A de S, el complemento de A es un conjunto de todos los miembros de S que no sean miembros del A.

Si el conjunto B es el complemento de A, escriba B = A'. La definición del complemento de A en S se escribe en la notación del conjunto como A\S = {x ∈ B | x ∈ S and x ∉ A }.

Teoremas del complemento

A\(B ∩ C) = (A\B) ∪ (A\C)

El complemento de una intersección de conjuntos es igual a la unión del complemento de cada conjunto.

DeclaraciónJustificación
A\(B ∩ C) ={x | x ∈ A and x ∉ (B ∩ C)}Traduzca para notación del conjunto.
{x | x ∈ A and (x ∉ B or x ∉ C)}Intersección de conjuntos
{x | ( x ∈ A and x ∉ B ) or ( x ∈ A and x ∉ C)}Característica distributiva
((A\B) ∪ (A\C)Traduzca de nuevo a la notación algebraica
Cuadro 1: Complemento de la intersección de dos conjuntos.

A\(B ∪ C) = (A\B) ∪ (A\C)

El complemento de una unión de conjuntos es igual a la intersección del complemento de cada conjunto.

DeclaraciónJustificación
A\(B ∪ C) ={x | x ∈ A and x ∉ (B ∪ C)}Traduzca para notación del conjunto.
{x | x ∈ A and (x ∉ B and x ∉ C)}Intersección de conjuntos
{x | (x ∈ A and x ∉ B) and (x ∈ A and x ∉ C)}Característica distributiva
(A\B) ∪ (A\C)Traduzca de nuevo a la notación algebraica
Cuadro 2: Complemento de la unión de dos conjuntos.

Leyes de De Morgan

Ley de De Morgan para la intersección de conjuntos - (A ∩ B)' = A' ∪ B'

El complemento de una intersección de conjuntos es igual a la unión de los complementos de los conjuntos.
Una serie de imágenes que ilustran la ley de De Morgan para la intersección. Una serie de imágenes que ilustran la ley de De Morgan para la intersección.
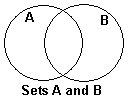
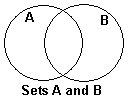
Cuadro 5: Chasque encendido las imágenes para ver representaciones de (A ∩ B)' = A' ∪ B'

Prueba de Theorem de De Morgan para la intersección de conjuntos
IlustraciónDeclaraciónJustificación
Pruebe eso (A ∩ B)' = A' ∪ B' demostrando eso (A ∩ B)' y A' ∪ B' es subconjuntos de uno a.Demanda
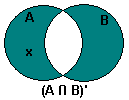Ilustración de x en el complemento de la intersección B. de A.Deje el x ∈ (A ∩ B)'Asunción
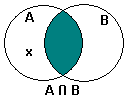Ilustración de x no en la intersección B. de A.Entonces x ∉ (A ∩ B)Definición del complemento de un conjunto
Ilustración de x no en la intersección B. de A.Por lo tanto x ∉ A o x ∉ B.Definición de la intersección de un conjunto.
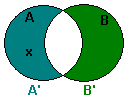Ilustración de x no en A o B'.Tan x ∈ A' o x ∈ B'Definición del complemento de un conjunto.
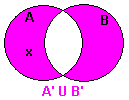Ilustración de x no en la unión B'. de A.Tan x ∈ (A' ∪ B')Definición de la unión de un conjunto.
Cuadro 3: Ley de De Morgan para la intersección.

Ley de De Morgan para la unión de conjuntos - (A ∪ B)' = A' ∩ B'

El complemento de una unión de conjuntos es igual a la intersección de los complementos de los conjuntos.
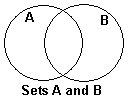
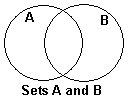
Una serie de imágenes que ilustran la ley de De Morgan para la unión. Una serie de imágenes que ilustran la ley de De Morgan para la unión.
Cuadro 6: Chasque encendido las imágenes para ver representaciones de ((A ∪ B)' = A' ∩ B'
Prueba de Theorem de De Morgan para la unión de conjuntos
IlustraciónDeclaraciónJustificación
Pruebe eso (A ∪ B)' = A' ∩ B'.Demanda
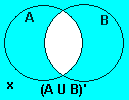Ilustración de x en el complemento de la intersección B. de A.Deje el x ∈ (A ∪ B)'Asunción
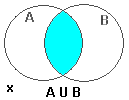Ilustración de x no en la intersección B. de A.Entonces x ∉ (A ∪ B)Definición del complemento de un conjunto
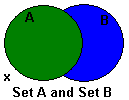Ilustración de x no en la intersección B. de A.Por lo tanto x ∉ A y x ∉ B.Definición de la unión de un conjunto.
Ilustración de x no en A o B'.Tan x ∈ A' y x ∈ B'Definición del complemento de un conjunto.
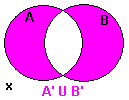Ilustración de x no en la unión B'. de A.Tan x ∈ (A' ∩ B')Definición de la intersección de un conjunto.
Cuadro 3: Ley de De Morgan para la unión.

Citar este artículo como:


Complemente (conjunto). 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/c/complementset.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-07-08: Primer párrafo ampliado y simplificado (McAdams, David.)
2008-03-31: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License