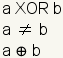Enciclopedia de Todas las Palabras de la Matemáticas Home Page -

Or-exclusiva

a	b
verdad	verdad	falso
verdad	falso	verdad
falso	verdad	verdad
falso	falso	falso
Cuadro 1: Tabla de la or-exclusiva de verdad.

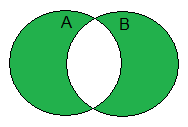
La or-exclusiva es una operación lógica que vuelve verdad solamente si un operando es verdad y el otro es falso. Para los asuntos a y b, la or-exclusiva es verdad si a o b es verdad, pero no ambas. El cuadro 1 es la tabla de verdad para la or-exclusiva. La or-exclusiva se puede también llamar una disyunción exclusiva. Al hablar, el término “or-exclusiva�? se abrevia a veces como “xor�?, pronunciado “ex-or�?.

Tres maneras en las cuales exclusivas o se pueden escribir son: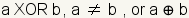 a xor b, a?b, o a?b

. En muchos lenguajes de programación, la or-exclusiva se denota con el símbolo del signo de intercalación (^). En electrónica, se dibuja una or-exclusiva una puerta como:

El diagrama de Venn con solamente las partes de a y de b que no están en campo común coloreó adentro.

Cuadro 1: Diagrama de Venn de a xor B.

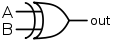Características de la or-exclusiva

Característica Usando palabras	Característica Usando símbolos	Descripción
a xor falso = a	a⊕false = a
a xor verdad = no a	a⊕true = ¬a
a xor a = falso	a⊕a = falso	La definición de la or-exclusiva implica que si ambos operandos son verdades, o ambos operandos son falsos, después or-exclusiva las vueltas falsas. `a=a`, un `a ≠ a` necesidad sea siempre falso.
a xor no a = verdad	a⊕¬a = verdad	La definición de la or-exclusiva de los estados que si los dos operandos no son iguales, or-exclusiva vueltas verdades. Desde el a⊕not a, a xor no a es siempre verdad.
a xor b = b xor a	a⊕b = b⊕a	La or-exclusiva es comutativa.
a xor (b xor c) = (a xor b) xor c	a⊕(b⊕c) = (a⊕b)⊕c	La or-exclusiva es asociativa.
a xor b = no a xor no b	a⊕b = ¬a⊕¬b	Si el valor de verdad de ambos operandos se intercambia, la or-exclusiva todavía vuelve el mismo valor.
no (a xor b) = no a xor b = a xor no b	¬(a⊕b) = ¬a⊕b = a⊕¬b	La negada lógica de la or-exclusiva del resultado es la misma cosa que negando uno de los operandos de la or-exclusiva.
a xor b = (a y no b) o (no a y b)	a⊕b = (a∧¬b)∨(¬a∧b)	Ésta es una nueva exposición de la definición de la or-exclusiva: una or-exclusiva una operación es verdad solamente si una de las discusiones es verdad y la otra es falsa.
a xor b = (a o b) y (no a o no b)	a⊕b = (a∨b)∧(¬a∨¬b)	Ésta es otra vez una nueva exposición de la definición de la or-exclusiva. El primer término `(a o b)` es verdad si `a` o `b` es verdad. El segundo término `(no a o no b)` es verdad si tampoco a y b es falsos. Con la conjunción, la expresión entera es verdad si a o b es verdad.
a xor b = (a o b) y no (a y b)	a⊕b = (a∨b)∧¬(a∧b)	Ésta es otra nueva exposición de la definición de la or-exclusiva.
Cuadro 2: Características de la or-exclusiva.

Bitwise or-exclusiva

En lógica, los operandos de la or-exclusiva deben ser un valor de verdad, deben ser cualquiera verdad de falso. En computadoras, los operandos de la or-exclusiva son números binarios. La or-exclusiva se aplica a los pedacitos correspondientes de los operandos:

0 xor 0 = 0; 0 xor 1 = 1; 1 xor 0 = 1; 1 xor 1 = 0; 1001 xor 1100 = 0110

Citar este artículo como:

Or-exclusiva. 2009-04-18. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/e/exclusiveor.html.

Traducciones

Click here to see this article in English.

créditos de imagen

Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión

2009-04-18: Discusión corregida de a xor a. (McAdams, David.)
2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2009-01-08: Versión inicial (McAdams, David.)

#	A	B	C	D
E	F	G	H	I
J	L	M	N	O
P	Q	R	S	T
U	V	X	Y

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License