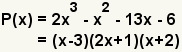Descomponer en factores polinomios: Encontrar todos los factores de un polinomio.

Descomponer en factores polinomios

P (x)=2x^3-x^2-13x-6= (x-3) (2x=1) (x+2)
Cuadro 1: Un polinomio descompuesto en factores.

Para descomponer en factores un polinomio es encontrar dos o más factores de un polinomio. Los factores de un polinomio son un sistema de polinomios de pocos o igualan grado que, cuando están multiplicados juntos, hagan el polinomio original. Para descomponer en factores un polinomio es totalmente encontrar los factores de menos grado que, cuando están multiplicados juntos, hacen el polinomio original.

Indicado matemáticamente, para descomponer en factores un polinómico P(x), es encontrar dos o más polinomios, diga Q(x) y R(x), de poco grado tales que P(x) = Q(x)·R(x). En el ejemplo 1, x-3, 2x+1, y (x+2) es los factores del polinómico 2x3 - x2 - 13x - 6.

Descomponer en factores el paso 1: Descomponga en factores hacia fuera el máximo común divisor

Para descomponer en factores un polinomio, el primeros encuentran el máximo común divisor de los términos. El máximo común divisor se puede encontrar cerca:

  1. Encontrar la facturización primera de cada uno de los términos.
  2. Identificación de los factores comunes.
  3. Multiplicando los factores comunes juntos para conseguir el máximo común divisor.

PasoFiguraDescripción
1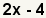2x-4Éste es el polinomio a descomponer en factores.
2Encuentre el máximo común divisor de los términos.
2.12x=2*x, -4=-2*2Encuentre la facturización primera de los términos. Los factores primeros de 2x son 2 y x. Los factores primeros de 4 son 2 y 2. El -1 se utiliza para preservar la muestra. Puesto que el valor de x es desconocido, para los propósitos de descomponer en factores, se toma para ser primero.
2.22x=2*x, -4=-2*2 con los factores “2� destacados.Identifique los factores comunes. En este caso, 2 es el único factor común.
2.3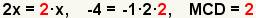2x=2*x, -4=-2*2, MCD=2, con los “2� destacados.Calcule el máximo común divisor (MCD). Puesto que el único factor común es 2, el máximo común divisor debe también ser 2.
3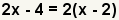2x-4 = 2 (2x-2)Reescriba el polinomio como el máximo común divisor multiplicado por cada uno de los términos con el máximo común divisor quitado.
42 (2x-2) =2*2x-2*2=4x-4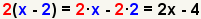Compruebe el trabajo multiplicando los polinomios usando la propiedad distributiva de la multiplicación.
Ejemplo 1

PasoFiguraDescripción
1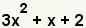3x^2+x+2Éste es el polinomio a descomponer en factores.
2Encuentre el máximo común divisor de los términos.
2.1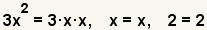3x^2=3*x*x, x=x, 2=2Encuentre la facturización primera de los términos. Los factores primeros de 3x2 son 3·x·x. El factor primero de x es x. El factor primero de 2 es 2. Puesto que el valor de x es desconocido, para los propósitos de descomponer en factores, se toma para ser primero.
2.23x^2=3*x*x, x=x, 2=2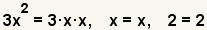.Identifique los factores comunes. En este caso, 1 es el único factor común. Puesto que un factor de 1 no es útil, se hace este paso.
Ejemplo 2

PasoFiguraDescripción
1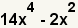14x^4-2x^2Éste es el polinomio a descomponer en factores.
2Encuentre el máximo común divisor de los términos.
2.1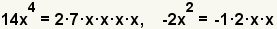14x^4=2*7*x*x*x*x, -2x^2=-1*2*x*xEncuentre la facturización primera de los términos. Los factores primeros de 14x4 son 2·7·x·x·x·x. Los factores primeros de 2x2 son 2·x·x. El -1 se utiliza para preservar la muestra. Puesto que el valor de x es desconocido, para los propósitos de descomponer en factores, se toma para ser primero.
2.2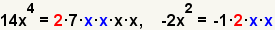14x^4=2*7*x*x*x*x, -2x^2=-1*2*x*x con los factores “2� destacados y dos factores “x� destacados.Identifique los factores comunes. En este caso, 2, x y x son los factores primeros comunes.
2.3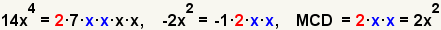14x^4=2*7*x*x*x*x, -2x^2=-1*2*x*x, MCD=2*x*x=2x^2 con los factores “2� destacados y dos factores “x� destacados.Calcule el máximo común divisor (MCD). Puesto que los factores primeros comunes son 2, x y x, el máximo común divisor es 2·x·x = 2x2.
3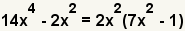14x^4-2x^2 = 2x^2 (7x^2-1)Reescriba el polinomio como el máximo común divisor multiplicado por cada uno de los términos con el máximo común divisor quitado.
4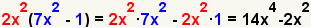2x^2 (7x^2-1) =2x^2*7x^2+2x^2* (- 1) =14x^4-2x^2Compruebe el trabajo multiplicando los polinomios usando la propiedad distributiva de la multiplicación.
Ejemplo 3

Descomponer en factores polinomios del grado 2 usando la fórmula cuadrático

El segundo paso en descomponer en factores un polinomio del grado 2, también llamado una ecuación cuadrático, es determinar si puede ser descompuesto en factores usando números reales. El discriminante de un polinomio del grado 2 dice cuántos y qué tipos de soluciones se pueden encontrar para una ecuación cuadrático. Para una ecuación cuadrático f(x) = ax2 + bx + c, el discriminante es b2 - 4ac.

DiscriminanteSolucionesEjemplo
b2 - 4ac < 0Dos soluciones complejas; Ningunas soluciones reales.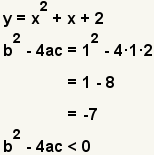y=x^2+x+2, b^2-4ac=1^1-4*1*2=1-8=-7, b^2-4ac<0
b2 - 4ac = 0Una solución real.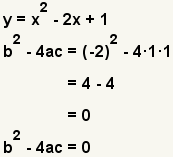y=x^2-2x+1, b^2-4ac= (- 2) ^1-4*1*1=4-4=0, b^2-4ac=0
b2 - 4ac > 0Dos soluciones reales.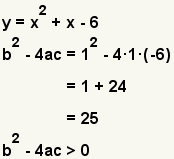y=x^2+x-6, b^2-4ac=1^1-4*1* (- 6) =1+24=25, b^2-4ac>0
Cuadro 1: Discriminante y soluciones de una ecuación cuadrático

Si no hay soluciones reales, la ecuación cuadrática no puede ser descompuesta en factores más lejos sin usar números complejos. Si hay soluciones reales, utilice la función cuadrático para encontrar las soluciones.

Descomponer en factores una ecuación cuadrática con dos soluciones reales

EcuaciónDescripción
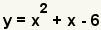y=x^2+x-6Ésta es la ecuación a descomponer en factores.
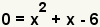0=x^2+x-6Puesto que estamos encontrando las raíces del polinómico, fije y a 0.
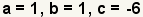a=1, b=1, c=-6Identifique a, b, y c en la función cuadrático. a = 1 y b = 1 puesto que los coeficientes implicados de x2 y de x son 1.
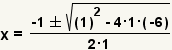x= (- raíz 1+-square (1^2-4*1* (- 6)))/(2*1)Complete la fórmula cuadrático.
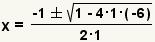x= (- raíz 1+-square (1-4*1* (- 6)))/(2*1)Simplifique el exponente.
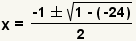x= (- raíz 1+-square (1 (- 24)))/2Simplifique la multiplicación.
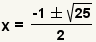x= (- raíz 1+-square (25))/2Simplifican la suma y la resta.
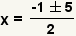x= (- 1+-5) /2Simplifique la raíz cuadrada.
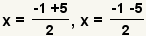x= (- 1+5)/2, x= (- 1-5) /2Parta la solución en dos ecuaciones explícitas.
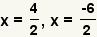x=4/2, x=-6/2Simplifique los numeradores.
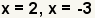x=2, x=-3Simplifique las fracciones.
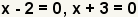x-2=0, x+3=0Consiga cero en un lado de la ecuación hacer los factores.
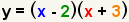y= (x-2) (x+3)Reescriba la ecuación usando los factores.
y=x*x+x*3+x* (- 2) + (- 2) (3)Compruebe el trabajo.
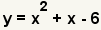y=x^2+x-6Simplifique los términos y agregue términos semejantes. Ésta es la ecuación original, así que el descomponer en factores está correcto.
Ejemplo 4.

Descomponer en factores una ecuación cuadrática con una solución real

EcuaciónDescripción
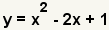y=x^2-2x+1Ésta es la ecuación a descomponer en factores.
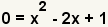0=x^2-2x+1Puesto que estamos encontrando las raíces del polinómico, fije y a 0.
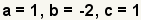a=1, b=-2, c=1Identifique a, b, y c en la función cuadrático. a = 1 puesto que el coeficiente implicado de x2 es 1.
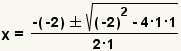x= (- (- 2) raíz de +-square ((- 2) ^2-4*1*1))/(2*1)Complete la fórmula cuadrático.
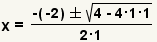x= (2+-square raíz (4-4*1*1))/(2*1)Simplifique el exponente.
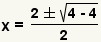x= (raíz 2+-square (4-4))/2Simplifique la multiplicación.
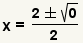x= (raíz 2+-square (0))/2Simplifique la suma y la resta.
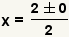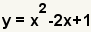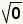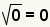x= (2+-0) /2Puesto que La raíz cuadrada de -7 iguala la raíz cuadrada (7) del I., substituya raíz cuadrada (7) i para Raíz cuadrada de (-7)..
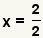x=2/2Puesto que es cualquier cosa más cero sí mismo y es cualquier cosa menos cero sí mismo, el más o menos cero sale.
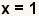x=1Reduzca la fracción.
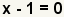x-1=0Reste 1 de ambos lados para conseguir el factor.
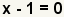y= (x-1) (x-1)Ponga los factores en escrito. Puesto que hay solamente una raíz del polinomio, es una raíz doble.
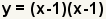y=x*x-1x-1x+1Compruebe el trabajo.
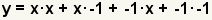y=x^2-2x+1Simplifique los términos y agregue términos semejantes. Ésta es la ecuación original, así que el descomponer en factores está correcto.
Ejemplo 5.

Descomponer en factores una ecuación cuadrática sin soluciones reales

Si la gama de la ecuación se limita a los números reales, una ecuación cuadrática sin soluciones reales no se puede descomponer en factores más lejos. El ejemplo 4 demuestra cómo solucionar una ecuación cuadrático sin soluciones reales.

EcuaciónDescripción
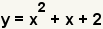y=x^2+x+2Ésta es la ecuación a descomponer en factores.
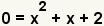0=x^2+x+2Puesto que estamos encontrando las raíces del polinómico, fije y a 0.
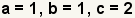a=1, b=1, c=2Identifique a, b, y c en la función cuadrático. a = 1 y b = 1 puesto que los coeficientes implicados de x2 y de x son 1.
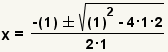x= (- 1+-square raíz (1^2-4*1*2))/(2*1)Complete la fórmula cuadrático.
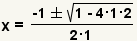x= (- 1+-square raíz (1-4*1*2))/(2*1)Simplifique el exponente.
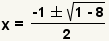x= (- raíz 1+-square (1-8))/2Simplifique la multiplicación.
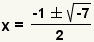x= (- raíz 1+-square (- 7))/2Simplifican la suma y la resta.
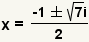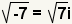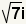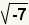x= (- 1+-square raíz (7) i) /2Puesto que La raíz cuadrada de -7 iguala la raíz cuadrada (7) I., substituya raíz cuadrada (7) i para Raíz cuadrada de -7x..
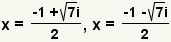x= (- raíz 1+square (7) i), x= (- 1-square raíz /2 (7) i) /2Parta la solución en dos ecuaciones explícitas.
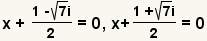x+ (1-square raíz (7) i) /2)=0, x+ (1+square raíz (7) i) /2)=0Consiga 0 en un lado de la ecuación para conseguir los factores.
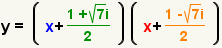y= (x+ (raíz 1-square (7) i) /2)) (x+ (raíz 1+square (7) i) /2)=0)Reescriba la ecuación usando los factores.
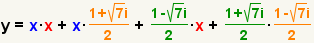y=x*x-1x-1x+1Compruebe el trabajo.
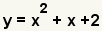y=x^2-2x+1Simplifique los términos y agregue términos semejantes. Ésta es la ecuación original, así que el descomponer en factores está correcto.
Ejemplo 6.

Descomponer en factores polinomios con el grado 3 o mayor

Las fórmulas para solucionar polinomios con el grado 3 y el grado 4 son tan complicadas, eso que son solamente útiles en programas de computadora. Los polinomios del grado 5 y más alto no se pueden solucionar con una fórmula. El teorema fundamental de la álgebra implica que cada polinomio no-constante con coeficientes verdaderos se puede descomponer en factores sobre los números reales en un producto de factores lineares y de factores cuadráticos irreducibles. Mientras que el teorema fundamental de la álgebra dice los factores existen, él no nos dicen cómo encontrarlos. Hay muchos métodos que pueden ser utilizados. El teorema racional de las raíces se puede utilizar para encontrar raíces posibles de un polinomio. La interpolación es otro método que se puede utilizar para encontrar las raíces de un polinomio. Las soluciones gráficas pueden también aproximar raíces y factores de un polinomio.

Más información

  • McAdams, David. El solucionar gráficamente. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. https://www.allmathwords.org/es/g/graphicalsolutions.html.
  • McAdams, David. Interpolación. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. https://www.allmathwords.org/article.aspx?lang=es&id=Interpolation.
  • McAdams, David. Teorema racional de las raíces. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. https://www.allmathwords.org/article.aspx?lang=es&id=Rational%20Roots%20Theorem.

Citar este artículo como:
Descomponer en factores polinomios. 2009-05-04. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/f/factoringpolynomials.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-05-04: Texto corregido por ejemplo 2. (McAdams, David.)
2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2009-01-20: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License