Desigualdad: Una relación de equivalencia usando <>=, >.

Desigualdad

Una desigualdad es una relación de equivalencia que utiliza a uno de los operadores siguientes de la relación:
OperadorDescripciónGráfico
<Menos queCírculo hueco en una Recta numérica con una flecha a la izquierda.
≤
<=		Inferior o igualCírculo sólido en una Recta numérica con una flecha a la izquierda.
≠
!=
#		No igual a; Esto se podía también llamar menos que o mayor que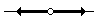Círculo hueco en una Recta numérica con una flecha a la izquierda y a la derecha.
≥
>=		Mayor o igualCírculo sólido en una Recta numérica con una flecha a la derecha.
>Mayor queCírculo hueco en una Recta numérica con una flecha a la derecha.
Cuadro 1: Operadores de la desigualdad

Una desigualdad compuesta tiene más de un operador de la desigualdad.

Las desigualdades se pueden solucionar como igualdades con una suma importante: Si la desigualdad es multiplicada por un número negativo, < cambios a > y > cambios a <. ahora multiplican ambos lados por -1, pero no cambian '>' a '<'. Comience con la ecuación -16 < 5. Ahora multiplique ambos lados por -1 sin el cambio < a >. -1·-16 < -1·5 se convierte a 16 < -5 cuál es falso.

Representación gráfica de desigualdades de una variable

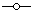Al representar desigualdades de una variable gráficamente en una Recta numérica, comience con las puntos finales. Si la variable puede ser igual a la punto final, dibuje un circunferencia sólido en la Recta numérica: Circunferencia sólido. Si la variable no puede ser igual a la punto final, dibuje un circunferencia hueco en la Recta numérica: Circunferencia hueco. Entonces dibuje las rectas que representan las desigualdades. El cuadro 2 demuestra algunos ejemplos.
EcuaciónGráficoExplicación
a < 5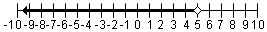Recta numérica con el circunferencia hueco en 5 con una flecha a la izquierda.Puesto que 5 es la punto final, el circunferencia está en 5. La desigualdad es “<� así que el circunferencia es hueco. Desde a < 5, la flecha va a la izquierda.
a ≤ -3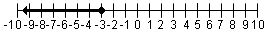Recta numérica con el circunferencia sólido en -3 con una flecha a la izquierda.Puesto que -3 es la punto final, el circunferencia está en -3. La desigualdad es “≤â€? así que el circunferencia es sólido. Desde a ≤ -3, la flecha va a la izquierda.
t ≥ 2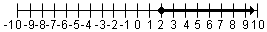Recta numérica con el circunferencia sólido en 2 con una flecha a la derecha.Puesto que 2 es la punto final, el circunferencia está en 2. La desigualdad es “≥â€? así que el circunferencia es sólido. Desde un t ≥ 2, la flecha va a la derecha.
t > -6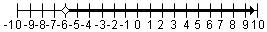Recta numérica con el circunferencia hueco en -6 con una flecha a la derecha.Puesto que -6 es la punto final, el circunferencia está en -6. La desigualdad es “>� así que el circunferencia es hueco. Desde t > -6, la flecha va a la derecha.
-4 < r ≤ 2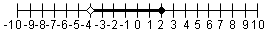Recta numérica con el circunferencia hueco en -4, un circunferencia sólido en 2, y una recta entre -4 y 2.Puesto que -4 y 2 es las puntos finales, los circunferencias están en -4 y 2. La desigualdad para -4 es '<' de modo que el circunferencia sea hueco. La desigualdad para 2 es “≤â€? de modo que el circunferencia sea sólido.
1 > r o r ≥ 3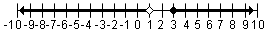Recta numérica con el circunferencia sólido en 1, un circunferencia hueco en 3, una flecha que va a la izquierda a partir de la 1 y una flecha que va a la derecha a partir del 3.Puesto que 1 y 3 es las puntos finales, los circunferencias están en 1 y 3. La desigualdad para 1 es '>' de modo que el circunferencia sea hueco. La desigualdad para 3 es “≥â€? de modo que el circunferencia sea sólido.
Cuadro 2: Gráficos de las desigualdades de una variable.

Solucionar desigualdades de una variable

Las desigualdades se solucionan mucho el igual estaban como igualdades. Aquí está un ejemplo que soluciona la desigualdad -x + 5 ≤ -5.
PasoDesigualdadExplicación
1-x + 5 ≤ -5Ecuación original
2-x + 5 - 5 ≤ -5 - 5 ⇒
-x ≤ -10		Reste 5 de ambos lados
3-1·-x ≥ -1·-10 ⇒
x ≥ 10		Multiplique ambos lados por -1. Puesto que la desigualdad está siendo multiplicada por un número negativo, cambie el ≤ al ≥.
411 ≥ 10Desde 11 ≥ 10, substituto 11 adentro para x en la ecuación original para comprobar el trabajo.
Cuadro 3: Solucionar una desigualdad

Citar este artículo como:


Desigualdad. 2009-04-17. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/i/inequality.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-17: Ecuaciones fijas en el ejemplo 3 (McAdams, David.)
2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-08-11: Errores tipográficos fijos (McAdams, David.)
2008-06-09: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License