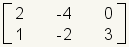Enciclopedia de Todas las Palabras de la Matemáticas Home Page -

Matriz

-- el plural es matrices.

Figura matriz del 1:2 x3

Una matriz se compone de los valores dispuestos en filas y columnas. En matemáticas avanzada, los valores pueden ser variables, ecuaciones u otras matrices. Este artículo se ocupará de las matrices que contienen solamente números.

�?ndice del artículo

Matriz
Dimensión de la matriz
Matriz cuadrada
Diagonal de una matriz cuadrada
Elemento de matriz
Elementos correspondientes
Suma de la matriz
Multiplicación escalar
Multiplicación de la matriz
Usando las matrices para solucionar sistemas lineares
Determinante de una matriz
Regla de Cramer

Matriz

Una matriz se utiliza para organizar datos. Una vez que los datos se organizan en una matriz, las operaciones estándar de la matriz se pueden realizar para manipular los datos. Aquí está un ejemplo de ventas al por menor. El cuadro 1 contiene la información de las ventas para los primeros tres meses del año para un almacén. El cuadro 2 contiene la información de las ventas para los segundos tres meses del año para el mismo almacén.

1r Ventas cuartas, almacén #482
	Enero	Febrero	Marzo
Fruta	$3045	$2997	$3200
Vehículos	$4056	$4227	$4509
Pastas	$2650	$3204	$3098
Lechería	$5345	$4723	$4933
Cuadro 2: Tabla de ventas del primer trimestre.

2do Ventas cuartas, almacén #482
	Abril	Mayo	Junio
Fruta	$3420	$3560	$3700
Vehículos	$4716	$4850	$4900
Pastas	$3274	$2840	$2760
Lechería	$4769	$4799	$4873
Cuadro 3: Tabla de ventas del segundo trimestre.

Estos cuadros 1 y 2 se pueden organizar en dos matrices:

Cuadro 4: Matriz que corresponde a la tabla en el cuadro 2.

Cuadro 5: Matriz que corresponde a la tabla en el cuadro 3.

Note que no se transfiere ningunas de las etiquetas a la matriz. Sin embargo, los números en las filas y las columnas todavía tienen el mismo significado. Todo en la primera fila es números de las ventas para la fruta. Todo en la segunda fila es números de las ventas para los vehículos. Todo en la primera columna es las ventas para el primer mes del cuarto.

Cheque de comprensión

Chasque encendido la caja de cheque de la respuesta que usted piensa está correcto.

¿Cuál es el significado de la matriz 2, fila 3?
Ventas de la fruta.
No, puesto que la fila 3 de la matriz 2 corresponde para remar tres del cuadro 2, la fila 3 representa ventas de las pastas.
Ventas de vehículos.
No, puesto que la fila 3 de la matriz 2 corresponde para remar tres del cuadro 2, la fila 3 representa ventas de las pastas.
Ventas de las pastas.
Sí, puesto que la fila 3 de la matriz 2 corresponde para remar tres del cuadro 2, la fila 3 representa ventas de las pastas.
Ventas de los productos lácteos.
No, puesto que la fila 3 de la matriz 2 corresponde para remar tres del cuadro 2, la fila 3 representa ventas de las pastas.
¿Cuál es el significado de la matriz 1, columna 2?
Ventas de enero.
No, puesto que la columna 2 de la matriz 1 corresponde a la columna 2 del cuadro 2, la fila 3 representa las ventas de febrero.
Ventas de febrero.
No, puesto que la columna 2 de la matriz 1 corresponde a la columna 2 del cuadro 2, la fila 3 representa las ventas de febrero.
Ventas de mayo.
Sí, puesto que la columna 2 de la matriz 1 corresponde a la columna 2 del cuadro 2, la fila 3 representa las ventas de febrero.
Ventas de junio.
No, puesto que la columna 2 de la matriz 1 corresponde a la columna 2 del cuadro 2, la fila 3 representa las ventas de febrero.
¿Cuál es el significado de la matriz 1, columna 1, fila 2?
Ventas de la fruta en enero.
No, desde la columna 1, la fila 2 de la matriz 1 corresponde a la columna 1, fila 2 del cuadro 1, esta célula representa ventas de vehículos en enero.
Ventas de vehículos en marzo.
No, desde la columna 1, la fila 2 de la matriz 1 corresponde a la columna 1, fila 2 del cuadro 1, esta célula representa ventas de vehículos en enero.
Ventas de la fruta en abril.
No, desde la columna 1, la fila 2 de la matriz 1 corresponde a la columna 1, fila 2 del cuadro 1, esta célula representa ventas de vehículos en enero.
Ventas de vehículos en mayo.
Sí, desde la columna 1, la fila 2 de la matriz 1 corresponde a la columna 1, fila 2 del cuadro 1, esta célula representa ventas de vehículos en enero.

Dimensión de la matriz

Cada matriz tiene una dimensión. Puesto que la matriz 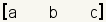Matriz con una fila y tres columnas. tiene 1 fila y 3 columnas, las dimensiones de esta matriz son 1x3.

Matriz	Número de filas	Número de columnas	Dimensiones
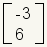	2	1	2x1
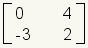	2	2	2x2
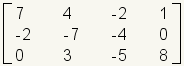	3	4	3x4
Cuadro 6: Dimensiones de matrices

Matriz cuadrada

Cuadro 7: Una matriz del cuadrado 2x2

Una matriz cuadrada es una matriz que tiene el mismo número de filas que columnas. Una propiedad de una matriz cuadrada es que una matriz cuadrada se puede multiplicar por sí mismo. Esto no es verdad para las matrices que no son cuadradas.

Diagonal de una matriz cuadrada

Cuadro 8: La diagonal de una matriz 3x3

La diagonal de una matriz cuadrada A es los elementos A [1.1], A [2.2], A [3.3],…. En el cuadro 8, la diagonal se destaca en rojo.

Elemento de matriz

Matriz A con el elemento en la segunda fila, primera columna destacada.

Cuadro 9: Matriz A

Cada entrada en una matriz se llama un elemento de matriz. Cada elemento es identificado por fila y la columna en el arsenal. El elemento destacado en la matriz A se identifica como A [2.1]. Esto significa el elemento en la segunda fila, primera columna de la matriz A.

Cheque de comprensión

Chasque encendido la caja de cheque de la respuesta que usted piensa está correcto.

¿Cuál es el valor del elemento A [3.2]?
1
No. El elemento en la fila 3 (cuenta abajo de 3 filas) y la columna 2 (cuenta sobre 2 columnas) tiene un valor de 4.
4
Sí. El elemento en la fila 3 (cuenta abajo de 3 filas) y la columna 2 (cuenta sobre 2 columnas) tiene un valor de 4.
5
No. El elemento en la fila 3 (cuenta abajo de 3 filas) y la columna 2 (cuenta sobre 2 columnas) tiene un valor de 4.
8
No. El elemento en la fila 3 (cuenta abajo de 3 filas) y la columna 2 (cuenta sobre 2 columnas) tiene un valor de 4.
¿Cuál es el valor del elemento A [1.3]?
1
No. El elemento en la fila 1 (cuenta abajo de 1 fila) y la columna 3 (cuenta sobre 3 columnas) tiene un valor de 7.
3
No. El elemento en la fila 1 (cuenta abajo de 1 fila) y la columna 3 (cuenta sobre 3 columnas) tiene un valor de 7.
5
No. El elemento en la fila 1 (cuenta abajo de 1 fila) y la columna 3 (cuenta sobre 3 columnas) tiene un valor de 7.
7
Sí. El elemento en la fila 1 (cuenta abajo de 1 fila) y la columna 3 (cuenta sobre 3 columnas) tiene un valor de 7.
¿Qué elemento de la matriz A tiene un valor de 1?
A [1.1]
No. El elemento A [2.2] = 1.
A [1.2]
No. El elemento A [2.2] = 1.
A [2.1]
No. El elemento A [2.2] = 1.
A [2.2]
Sí. El elemento A [2.2] = 1.

Elementos correspondientes

Los elementos correspondientes en matrices son elementos con la misma fila y columna. En el cuadro 10, los elementos correspondientes de las dos matrices son el mismo color.

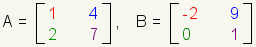Cuadro 10: Elementos correspondientes

Suma de la matriz

La suma des matries se define como suma de elementos correspondientes. Deje la matriz

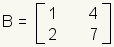
2x2 elementos que contienen 1, 4, 2, 7 de la matriz B

y matriz

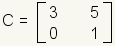
2x2 elementos que contienen 3, 5, 1, 0 de la matriz C

Para agregar la matriz B a C, agregue el valor de B [1.1] a C [1.1], B [1.2] a C [1.2], y así sucesivamente como sigue:

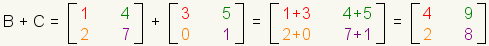suma de la matriz B y C para conseguir la matriz 2x2 que contiene 4.9.3.7.

Cuadro 11: Adición de la matriz

Puesto que cada elemento en la primera matriz debe tener un elemento correspondiente en la segunda matriz, sólo las matrices con las mismas dimensiones pueden ser agregadas. La suma de matrices con diversas dimensiones es indefinida. Esto significa que usted no puede agregar matrices con diversas dimensiones.

La resta des matrices es similar a la suma de la matriz. Reste los elementos correspondientes.

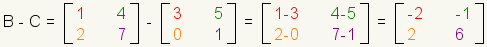Substracción de la matriz C de B para conseguir la matriz 2x2 que contiene -2, -1, 1, 7.

Cuadro 12: Substracción de la matriz

Multiplicación escalar

Una matriz que es multiplicada por los 5. escalares.

Cuadro 13: Multiplicación escalar

En la multiplicación escalar, un escalar es un número que es multiplicado por cada elemento de la matriz. El cuadro 13 demuestra los 5 escalares que son multiplicados por una matriz. Cada elemento de la matriz es multiplicado por cinco.

Multiplicación de la matriz

La multiplicación de la matriz se define como multiplicar los elementos de cada fila de la primera matriz por las columnas de cada columna de la segunda matriz. El cuadro 14 demuestra un ejemplo de la multiplicación de la matriz.

matriz [a11, a12, a13, a21, a22, a23] * [b11, b12, b21, b22, b31, b33] = [a11*b11+a12*b21+a13*b31, a11*b12+a12*b22+a13*b32, a21*b11+a22*b21+a23*b31, a21*b12+a22*b22+a23*b32]

Cuadro 14: Multiplicación de la matriz.

Para multiplicar dos matrices, deben ser compatibles. Esto significa que el número de columnas en la primera matriz debe ser igual que el número de columnas en la segunda matriz. El cuadro 15 da algunos ejemplos de matrices compatibles e incompatibles.

Matriz 1	Matriz 2	Compatibilidad
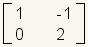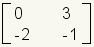		Compatible. Estas matrices son compatibles. Pueden ser multiplicadas. La primera matriz tiene 2 columnas y la segunda matriz tiene 2 filas.
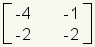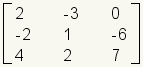		Incompatible. Estas matrices son incompatibles. No pueden ser multiplicadas. La primera matriz tiene 2 columnas y la segunda matriz tiene 3 filas.
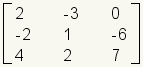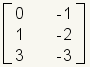		Compatible. Estas matrices son compatibles. Pueden ser multiplicadas. La primera matriz tiene 3 columnas y la segunda matriz tiene 3 filas.
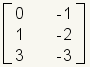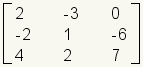		Incompatible. Estas matrices son incompatibles. No pueden ser multiplicadas. La primera matriz tiene 2 columnas y la segunda matriz tiene 3 filas. Nota: Éstas son las mismas matrices en el ejemplo anterior, pero se han invertido. Esto significa que la multiplicación de la matriz no es comutativa.
Cuadro 15: Compatibilidad de la matriz

Es más fácil recordar cómo multiplicar matrices si usted levanta la segunda matriz. Tome, por ejemplo, el problema de la multiplicación de la matriz:

¿matriz 3x3 multiplicada por la matriz 3x2 =?

La segunda matriz se levanta como esto:

Ahora las columnas y las filas de las matrices que serán multiplicadas se alinean. Comience con la fila 1 y la columna 1 de la matriz. Los elementos en la primera fila de la primera matriz son multiplicados por los elementos en la primera columna de la segunda matriz:

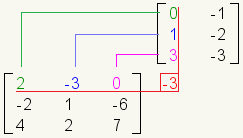
matriz 3x3 multiplicada por la matriz 3x2 con la primera fila de la primera matriz destacada y de la primera columna de la segunda matriz destacada.

2·0+ (- 3)·1+0·3 = 0-3+0 = -3. Ahora multiplique la fila 1 de la matriz 1 por la columna 2 de la matriz 2.

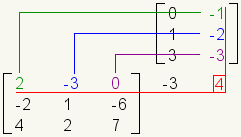
matriz 3x3 multiplicada por la matriz 3x2 con la primera fila de la primera matriz destacada y de la segunda columna de la segunda matriz destacada.

2·(- 1) + (- 3)·2+0·(- 3) = -2+6+0 = 4. Ahora multiplique la fila 2 de la matriz 1 por la columna 1 de la matriz 2.

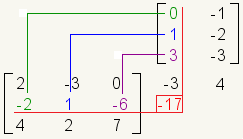
matriz 3x3 multiplicada por la matriz 3x2 con la segunda fila de la primera matriz destacada y de la primera columna de la segunda matriz destacada.

-2·(0) +1·1+ (- 6)·3 = 0+1-18 = -17. Continúe en el mismo patrón hasta que todas las filas de la primera matriz hayan sido multiplicadas por todas las filas de la segunda matriz.

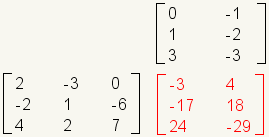
la matriz 3x3 multiplicó por la matriz 3x2 el resultado que era una matriz 3x2.

Éste es cómo la mirada del problema presentó horizontalmente:

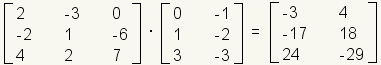
Más información

McAdams, David. Determinante de una estera. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. https://www.allmathwords.org/article.aspx?lang=es&id=Determinant%20of%20a%20Matrix.
McAdams, David. Regla de s de Cramer ''. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. https://www.allmathwords.org/article.aspx?lang=es&id=Cramer's%20Rule.
matriz. buscon.rae.es. Real Academia Española. 2009-04-03. http://buscon.rae.es/draeI/SrvltConsulta?TIPO_BUS=3&LEMA=matriz.

Citar este artículo como:

Matriz. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/m/matrix.html.

Traducciones

Click here to see this article in English.

créditos de imagen

Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión

2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-12-03: Agregado '' más información '', acoplamiento al determinante (McAdams, David.)
2008-11-17: Multiplicación agregada de la matriz (McAdams, David.)
2008-03-10: Versión inicial (McAdams, David.)

#	A	B	C	D
E	F	G	H	I
J	L	M	N	O
P	Q	R	S	T
U	V	X	Y

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License