Probabilidad: La probabilidad, la ocasión, o las probabilidades de un suceso del evento.

Probabilidad

La probabilidad es la probabilidad de un suceso del evento. Un otro sinónimo para la probabilidad son ocasión. Cuando usted dice, “estaré probablemente en la escuela mañana,� usted está diciendo que es probable usted estará en la escuela mañana, que hay una buena ocasión que usted estará en la escuela mañana.

Notación

La notación P(A) se utiliza para demostrar probabilidad. Para escribir que la probabilidad de la lluvia es el 50%, escriba P(lluvia) =0.5. Observar que un número devérticel está utilizado, no un porcentaje.

En probabilidad, hablamos o utilizamos:

  • Evento: Una ocurrencia sobre la cual se mide la probabilidad, calculado, o estimado.
  • Experimento: Un experimento está haciendo algo que hace que ocurre un evento.
  • Resultado: Un resultado es unidireccional un evento puede ocurrir.
  • Espacio muestral: Un espacio muestral es todos los resultados posibles.
  • Función de probabilidad: Una función que, cuando está dada un evento, vuelve una probabilidad estimada o real de esa ocurrencia del evento. Si uno agrega junto la probabilidad de todos los eventos, la suma debe ser 1 puesto que ésta refleja todas las posibilidades.
  • Gráfico de la distribución de probabilidad: Un gráfico que demuestra cómo la probabilidad de eventos se distribuye sobre el espacio muestral.

Ejemplo 1: águila o sello

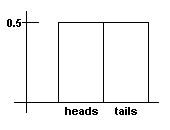
Cuando uno mueve de un tirón una moneda y registra el resultado, uno está haciendo un experimento en probabilidad. Las partes del experimento son:
ParteDescripción
ExperimentoEl experimento es el proceso entero de mover de un tirón la moneda y de registrar el evento.
EventoEl evento está moviendo de un tirón la moneda.
ResultadoEl resultado es cabezas o colas.
Espacio muestralEl espacio muestral es cabezas y colas. Uno puede escribir esto en la notación del conjunto como {las cabezas, las colas}.
Función de probabilidadP(cabezas) = 0.5, P(colas) = 0.5. Esto significa que la mitad del tiempo (0.5 = 1/2), la moneda sube las cabezas y mitad del tiempo que sube las colas. La suma de todas las posibilidades es 0.5 + 0.5 = 1
P(x)Combinaciones posiblesFracciónDevérticel
P(H)Moneda que demuestra las cabezas1/20.5
P(T)Moneda que demuestra las colas1/20.5
Gráfico de la distribución de probabilidad
Gráfico de la distribución de probabilidad que demuestra P(cabezas)=0.5, P(colas)=0.5.
Cuadro 1: Distribución de probabilidad de un tirón de la moneda.

Este gráfico de la distribución de probabilidad representa cómo la probabilidad de cada evento se distribuye sobre el espacio muestral entero. En este caso las probabilidades de cabezas son apenas iguales que las probabilidades de colas.

Ejemplo 2: águila o sello

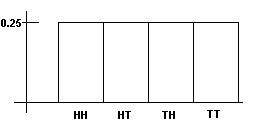
Cuando uno mueve de un tirón ambas monedas y registra el resultado, uno está haciendo un experimento en probabilidad. Las partes del experimento son:
ParteDescripción
ExperimentoEl experimento es el proceso entero de mover de un tirón monedas y de registrar el evento. Observe que esto podría también ser hecha moviendo de un tirón la misma moneda dos veces.
EventoEl evento está moviendo de un tirón ambas monedas.
ResultadoEl resultado es uno de: ambas águila, sello y águila, águila y sello, o ambas sello. Esto se puede abreviar como AA, SA, AS, y el SS donde “A� representa águilas y “S� representa sellos.
Espacio muestralHay 4 resultados en el espacio muestral. En la notación del conjunto esto es {AA, AS, SA, SS}.
Función de probabilidadP(AA)=0.25, P(AS)=0.25, P(SA)=0.25, P(SS)=0.25. Cada uno de los cuatro resultados tiene la misma probabilidad, o probabilidad, de la ocurrencia. La probabilidad de cada uno es tan 1/4 = 0.25. La suma de todas las posibilidades es 0.25 + 0.25 + 0.25 + 0.25 = 1.0.
P(x)Combinaciones posiblesFracciónDevérticel
P(AA)Moneda que demuestra las cabezasEspacio en blancoMoneda que demuestra las cabezas1/40.25
P(AS)Moneda que demuestra las cabezasEspacio en blancoMoneda que demuestra las colas1/40.25
P(SA)Moneda que demuestra las colasEspacio en blancoMoneda que demuestra las cabezas1/40.25
P(SS)Moneda que demuestra las colasEspacio en blancoMoneda que demuestra las colas1/40.25
Gráfico de la distribución de probabilidad
Gráfico de la distribución de probabilidad que demuestra P(AA)=0.25, P(AS)=0.25, P(SA)=0.25, P(SS)=0.25.
Cuadro 2: Distribución de probabilidad de mover de un tirón dos monedas

Este gráfico de la distribución de probabilidad representa cómo la probabilidad de cada evento se distribuye sobre el espacio muestral entero. En este caso las probabilidades cada uno de los resultados son iguales.

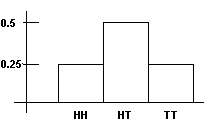
¿Qué si uno no cuida sube qué moneda las águilas y sube qué moneda las sellos? Entonces las sellos entonces las águilas (SA) son iguales que las águilas entonces las sello (AS). Esto significa que hay 3 resultados: AA, AS, SS. Las partes del experimento entonces están:
ParteDescripción
ExperimentoEl experimento es el proceso entero de mover de un tirón monedas y de registrar el evento. Observe que esto podría también ser hecha moviendo de un tirón la misma moneda dos veces.
EventoEl evento está moviendo de un tirón ambas monedas.
ResultadoEl resultado es uno de: ambas águila, águila y sello, o ambas sellos. Esto se puede abreviar como AA, AS, y el SS donde “A� representa águilas y “S� representa sellos.
espacio muestralHay 3 resultados en el espacio muestral. En la notación del conjunto esto es {AA, AS, SS}.
Función de probabilidadP(AA)=0.25, P(AS)=0.5, P(SS)=0.25. Puesto que hay el que está en la ocasión cuatro (P=0.25) del las águilas entonces las sellos y el que está en la ocasión cuatro del las sellos entonces las águilas, cuando éstos se combinan juntos, agregamos 0.25 + 0.25 = 0.5. La suma de todas las posibilidades es 0.25 + 0.5 + 0.25 = 1.
P(x)Combinaciones posiblesFracciónDevérticel
P(AA)Moneda que demuestra las cabezasEspacio en blancoMoneda que demuestra las cabezas1/40.25
P(AS)Moneda que demuestra las cabezasEspacio en blancoMoneda que demuestra las colas o Moneda que demuestra las colasEspacio en blancoMoneda que demuestra las cabezasel 1/20.5
P(SS)Moneda que demuestra las colasEspacio en blancoMoneda que demuestra las colas1/40.25
Gráfico de la distribución de probabilidad
Gráfico de la distribución de probabilidad que demuestra P (HH) =0.25, P (HT) =0.5, P (TT) =0.25.
Cuadro 3: Distribución de probabilidad de mover de un tirón 2 monedas.

Este gráfico de la distribución de probabilidad representa cómo la probabilidad de cada evento se distribuye sobre el espacio muestral entero. En este caso las probabilidades cada uno de los resultados no son iguales.

Ejemplo 3: Rueda de dos dados

Primera moneda.Segunda moneda

Ahora heche una ojeada los dados del balanceo dos. Generalmente uno no cuida que mueren tienen que valoran. Uno cuida solamente sobre la suma de los dados.
ParteDescripción
ExperimentoEl experimento es el proceso entero de rodar los dos dados y de registrar el evento. Observe que esto podría también ser hecha moviendo de un tirón la misma moneda dos veces.
EventoEl evento es dado del balanceo dos.
ResultadoPuesto que uno cuida solamente sobre el total de los dos dados, el resultado es uno del siguiente: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Espacio muestralHay 11 resultados en el espacio muestral, 2 a 12. En la notación del conjunto esto es {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
Función de probabilidadLa función de probabilidad para este experimento es:
P x)Combinaciones posiblesFracciónDevérticel aproximado
P(2) Dados que demuestran 1espacio en blancoDados que demuestran 1 1/360.0278
P(3) Dados que demuestran 1espacio en blancoDados que demuestran 2, Dados que demuestran 2espacio en blancoDados que demuestran 1 2/360.0556
P(4) Dados que demuestran 1espacio en blancoDados que demuestran 3 Dados que demuestran 2espacio en blancoDados que demuestran 2, Dados que demuestran 3espacio en blancoDados que demuestran 1 3/360.0833
P(5) Dados que demuestran 1espacio en blancoDados que demuestran 4 Dados que demuestran 2espacio en blancoDados que demuestran 3 Dados que demuestran 3espacio en blancoDados que demuestran 2, Dados que demuestran 4espacio en blancoDados que demuestran 1 4/360.1111
P(6) Dados que demuestran 1espacio en blancoDados que demuestran 5 Dados que demuestran 2espacio en blancoDados que demuestran 4 Dados que demuestran 3espacio en blancoDados que demuestran 3 Dados que demuestran 4espacio en blancoDados que demuestran 2, Dados que demuestran 5espacio en blancoDados que demuestran 1 5/360.1389
P(7) Dados que demuestran 1espacio en blancoDados que demuestran 6 Dados que demuestran 2espacio en blancoDados que demuestran 5 Dados que demuestran 3espacio en blancoDados que demuestran 4 Dados que demuestran 4espacio en blancoDados que demuestran 3 Dados que demuestran 5espacio en blancoDados que demuestran 2, Dados que demuestran 6espacio en blancoDados que demuestran 1 6/360.1667
P(8) Dados que demuestran 2espacio en blancoDados que demuestran 6 Dados que demuestran 3espacio en blancoDados que demuestran 5 Dados que demuestran 4espacio en blancoDados que demuestran 4 Dados que demuestran 5espacio en blancoDados que demuestran 3, Dados que demuestran 6espacio en blancoDados que demuestran 2 5/360.1389
P(9) Dados que demuestran 3espacio en blancoDados que demuestran 6 Dados que demuestran 4espacio en blancoDados que demuestran 5 Dados que demuestran 5espacio en blancoDados que demuestran 4, Dados que demuestran 6espacio en blancoDados que demuestran 3 4/360.1111
P(10) Dados que demuestran 4espacio en blancoDados que demuestran 6 Dados que demuestran 5espacio en blancoDados que demuestran 5, Dados que demuestran 6espacio en blancoDados que demuestran 4 3/360.0833
P(11) Dados que demuestran 5espacio en blancoDados que demuestran 6, Dados que demuestran 6espacio en blancoDados que demuestran 5 2/360.0556
P(12) Dados que demuestran 6espacio en blancoDados que demuestran 6 1/360.0278
El suma de todas las probabilidades junto da: 36/36 = 1.
Gráfico de la distribución de probabilidad
Gráfico de la distribución de probabilidad para los dados exagonales del balanceo 2.
Cuadro 4: Distribución de probabilidad para los dados exagonales del balanceo 2.

Este gráfico de la distribución de probabilidad representa cómo la probabilidad de cada evento se distribuye sobre el espacio muestral entero. En este caso las probabilidades cada uno de los resultados no son iguales.

Principios de probabilidad

Cuatro principios de base de la probabilidad son:

  • Al cuantificar, o diciendo el valor, de una probabilidad, utilizamos un número entre 0 y 1. En la notación algebraica, para un evento arbitrario A, 0 ≤ P(A) ≤ 1.
  • La probabilidad de un evento imposible es 0. Si el evento E es imposible, escribimos P(E)=0. Esto significa que la probabilidad de la ocurrencia de E es exactamente 0. En vida real, muy pocos eventos son absolutamente imposibles.
  • La probabilidad de un evento que suceda ciertamente es 1. Si el evento H está seguro, escribimos P(H) = 1.
  • La probabilidad de un evento que no sucede es 1 menos la probabilidad de ese suceso del evento. En la notación algebraica para un evento arbitrario A: P(!A) = 1 - P(A). Por ejemplo, si hay una ocasión del 30% de la lluvia hoy escribimos P(lluvia) = 0.3. Esto significa que la ocasión de la lluvia que no ocurre hoy es P(ninguna lluvia) = 1 - P(lluvia) = 1 - 0.3 = 0.7.

Más información

  • McAdams, David. Probabilidad. lifeisastoryproblem.com. Life is a Story Problem.org. 2009-04-03. Traducido automáticamente por babelfish.yahoo.com. http://www.lifeisastoryproblem.com/probability/index.html.
  • probabilidad. buscon.rae.es. Real Academia Española. 2009-04-03. http://buscon.rae.es/draeI/SrvltConsulta?TIPO_BUS=3&LEMA=probabilidad.

Citar este artículo como:
Probabilidad. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/p/probability.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-06-07: Deletreo corregido (McAdams, David.)
2008-04-14: Gráficos agregados de la distribución de probabilidad (McAdams, David.)
2008-04-12: Fraseología simplificada. Artículo reorganizado. Artículo ampliado con ejemplos (McAdams, David.)
2008-03-22: Revisado vea también para emparejar la especificación actual (McAdams, David.)
2007-07-12: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License