Alternate Interior Angles Theorem

Pronunciation: /ˈɔl.tər.nɪt ɪnˈtɪər.i.ər ˈæŋ.gəlz ˈθɪər.əm/ Explain

Click on the blue points and drag them to change the figure.

As the figure changes, what remains the same?
Manipulative 1 - Alternate Interior Angles Created with GeoGebra.

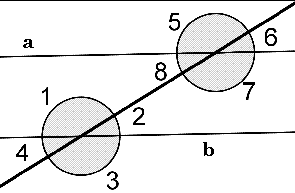
The Alternate Interior Angles Theorem states that if two parallel lines are cut by a transversal, then each pair of alternate interior angles is congruent.

Two parallel lines labeled 'a' and 'b'. A transversal line intersects both parallel lines. Eight angles formed by the intersections of the transversal with the parallel lines are labeled. On the lower intersection, starting with the upper right angle and going clockwise, the intersections are labeled 1, 2, 3, and 4. On the upper intersection, starting with the upper right angle and going clockwise, the angles are labeled 5, 6, 7, and 8.
Figure 2: Transversal.

Proof of the Alternate Interior Angles Theorem
StepDescriptionJustification
1 a || b This is a criterion, a necessary condition.
2 ∠1 ≅ ∠5 The Parallel Postulate states that, given a transversal of parallel lines, corresponding angles are congruent.
3 ∠5 ≅ ∠7 The Vertical Angle Congruence Theorem states that vertical angles are congruent.
4 ∠1 ≅ ∠7 The Transitivity of Congruence of Angles Theorem states that if two angles are congruent to the same angle, they are congruent to each other. In this case since ∠1 ≅ ∠5 and ∠5 ≅ ∠7, then ∠1 ≅ ∠7.
5 ∠2 ≅ ∠8
Q.E.D.		 A similar argument can be made to show that ∠2 ≅ ∠8.
Table 1: Proof of the Alternate Interior Angles Theorem

References

  1. McAdams, David E.. All Math Words Dictionary, Alternate Interior Angles Theorem. 2nd Classroom edition 20150108-4799968. pg 13. Life is a Story Problem LLC. January 8, 2015. Buy the book

Cite this article as:

 McAdams, David E. Alternate Interior Angles Theorem. 4/11/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/a/altinterioranglestheorem.html.

Image Credits

Revision History

4/11/2019: Changed equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/13/2018: Removed broken links, changed Geogebra links to work with Geogebra 5, updated license, implemented new markup. (McAdams, David E.)
5/5/2011: Initial version. (McAdams, David E.)

All Math Words Encyclopedia is a service of Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License