Associative Property of Addition

Pronunciation: /əˈsoʊ.siˌeɪ.tɪv ˈprɒp.ər.ti ʌv əˈdɪ.ʃən/ Explain

The associative property of addition states that, when adding three numbers, it does not matter in which order they are added. ^[2] This is expressed by the equation: a + (b + c) = (a + b) + c.

One way to remember the associative property of addition is to use the root word, 'associate'. So in the associative property of addition, the variables b and c associate closely on one side of the equals, while a and b associate closely on the other side.

A representation of the associative property of addition using dots is:

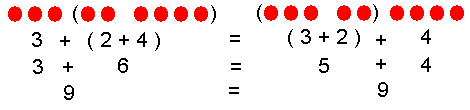Figure 1: 3+(2+4) = (3+2)+4 = 9.

Manipulative 1 contains a representation of the associative property of addition that uses the length of a line segment to represent each number. Notice that when the three segments are placed end to end, it doesn't matter which comes first, the total size is the same. Click on the end points and drag them to change the manipulative.

Click on the red, green, and blue points and drag them to change the figure. Why are the bottom three lines always the same length?

Manipulative 1 - Associative Property of Addition Created with GeoGebra.

The associative property of addition holds for real numbers, complex numbers, matrices of real and complex numbers, and vectors.

References

1. McAdams, David E.. All Math Words Dictionary, associative property of addition. 2nd Classroom edition 20150108-4799968. pg 21. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. Fine, Henry B., Ph. D.. Number-System of Algebra Treated Theoretically and Historically. 2nd edition. pg 5. www.archive.org. D. C. Heath & Co., Boston, U.S.A. 1907. Last Accessed 6/12/2018. http://www.archive.org/stream/thenumbersystemo17920gut/17920-pdf#page/n14/mode/1up/search/associative. Buy the book
3. Bettinger, Alvin K. and Englund, John A.. Algebra and Trigonometry. pg 2. www.archive.org. International Textbook Company. January 1963. Last Accessed 6/12/2018. http://www.archive.org/stream/algebraandtrigon033520mbp#page/n18/mode/1up. Buy the book

More Information

• McAdams, David E.. Associative. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 6/19/2018. https://www.allmathwords.org/en/a/associative.html.

Cite this article as:

McAdams, David E. Associative Property of Addition. 4/12/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/a/associativeaddition.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/12/2019: Changed equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/15/2018: Removed broken links, changed Geogebra links to work with Geogebra 5, updated license, implemented new markup. (McAdams, David E.)
12/19/2009: Added "References". (McAdams, David E.)
10/27/2008: Change manipulative from sketchpad to geogebra. (McAdams, David E.)
6/16/2008: Added 'Associative' to More Info. (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)