Boundary (Geometry)
Pronunciation: /ˈbaʊn.dri/ Explain
|
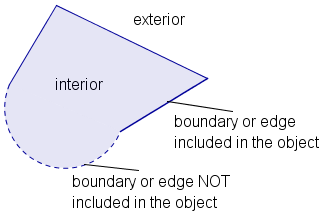
The boundary of a geometric figure is the set of points between the points in the figure and the points not in the figure. The exact mathematical definition of a boundary is given in terms of a set of boundary points. The definition of a boundary point is: Definition: A point is a boundary point of a figure if every neighborhood of the point contain at least one point in the figure and at least one point not in the figure. It is important here to note that every neighborhood must be considered. Visualize a point "close" to the boundary of a figure, but not on the boundary. From far enough away, it may seem to be part of the boundary, but as one "zooms in", a gap appears between the point and the boundary. Definition: The boundary of a geometric figure is the set of all boundary points of the figure. The concept of boundary can be extended to any ordered set of math objects. An element of an ordered set is a boundary element if all neighborhoods of the element contain at least one element in the figure and at least one element not in the figure. This generalization applies to sets of real numbers and sets of complex numbers. The concepts of open and closed can also be extended to ordered sets. The concepts of bounded and unbounded can be extended to ordered metric sets where the distance between two elements of the set is defined. |
Open or Closed
|
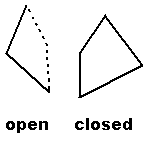
Note that the definition of a boundary does not require that a boundary point be part of the figure. If any boundary point is not part of a figure, then the figure is an open figure. If all boundary points are part of a figure, then the figure is a closed figure. Definition: A figure is closed if and only if all boundary points of the figure are part of the figure. A figure is open if it is not closed. By convention, an open boundary of a geometric figure is drawn with a dotted or dashed line. A closed boundary is drawn with a solid line. |
Interior, Exterior
|
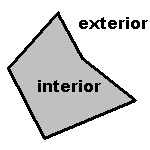
Definition: The interior of a geometric figure is all points that are part of the figure except any boundary points. The exterior of a geometric figure is all points that are not part of the figure except boundary points. Note that the interior of a figure may be the empty set. A figure may or may not have an interior. Take, for example, a line in a plane. Since a line is exactly one point thick, all the points on a line are boundary points of the line. Since an interior point can not be a boundary point, the line has no interior. The exterior of the line is all points in the plane except the line. |
Bounded or Unbounded
|
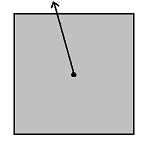
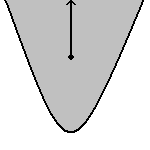
A geometric figure can be bounded or unbounded. Definition: A geometric figure is bounded if and only if the distance between any two points is finite. A geometric figure is unbounded if and only if it is not bounded. The distance between any two points is finite if there is a pair of points such that the distance between those two points is greater than or equal to the distance between any other pair of points in the figure. If a pair of points can always be found that is greater than any given pair of points, the figure is unbounded. Consider a square. If one picks any point in the square, and draws a ray from that point, the ray will eventually leave the square, no matter how big the square is. A square is bounded. Now consider a parabola. The interior of a parabola is the area between the lines of the parabola. Pick any point in the interior of the parabola. A ray can be drawn from that point that leaves the figure. However, a ray can also be drawn that never leaves the figure. A parabola is unbounded. Note that a figure that is unbounded still has a boundary. Unbounded simply means there is at least one ray that can be drawn that does not intersect a boundary. |
|
Example 1
|
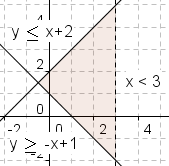
In figure 5, the line x = 3 is a boundary that is not part of the system of linear inequalities. The lines y = -x + 1 and y = x + 2 are boundaries that are part of the system of linear inequalities. |
References
- McAdams, David E.. All Math Words Dictionary, boundary. 2nd Classroom edition 20150108-4799968. pg 27. Life is a Story Problem LLC. January 8, 2015. Buy the book
Cite this article as:
McAdams, David E. Boundary (Geometry). 4/12/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/b/boundarygeometry.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/12/2019: Changed equations and expressions to new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/22/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
5/5/2011: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License