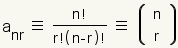Pascal's Triangle

Pronunciation: /pɑˈskɑlz ˈtraɪˌæŋ.gəl/ Explain

Pascal's triangle is a simplified version of the binomial theorem. Pascal's triangle starts at row 1 with the number 1. The second row contains two numbers: 1 and 1. In each iteration, adjacent values are added together to make the number for the next iteration.

Figure 2: Yang Hui triangle published in 1303 by Zhu Shijie. Click on the image to see a larger version.

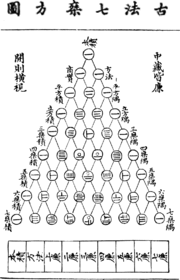
Pascal's triangle in the western world is named for the French mathematician Blaise Pascal. However, it was studied earlier in India, Persia, China, and Italy. See figure 2. Properties of Pascal's Triangle The sum of the numbers of each row is twice that of the previous row. The first number after the 1 in each row evenly divides all the other numbers if and only if the first number after the 1 is a prime number. The 'shallow diagonals' of Pascal's triangle add up to the Fibonacci numbers. See figure 3. The equation for Pascal's triangle is where n is the row number and r is the column in the row.

Figure 3: Shallow diagonals of Pascal's Triangle

References

1. McAdams, David E.. All Math Words Dictionary, Pascal's triangle. 2nd Classroom edition 20150108-4799968. pg 135. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. pascal's triangle. merriam-webster.com. Encyclopedia Britannica. Merriam-Webster. Last Accessed 12/3/2018. http://www.merriam-webster.com/dictionary/pascal's triangle. Buy the book

Cite this article as:

McAdams, David E. Pascal's Triangle. 4/27/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/p/pascalstriangle.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
• Yang Hui triangle published in 1303: Zhu Shijie, https://en.wikipedia.org. This work is in the public domain in its country of origin and other countries and areas where the copyright term is the author's life plus 100 years or less. https://en.wikipedia.org/wiki/File:Yanghui_triangle.gif.

Revision History

4/27/2019: Changed equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/1/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
10/25/2008: Initial version. (McAdams, David E.)