Plane

Pronunciation: /pleɪn/ Explain

A plane is a two dimensional space with infinite length and width, and no thickness. In Euclidean geometry, a plane is considered to be "flat". In other geometries, a plane may or may not be flat.

In Euclidean geometry, a plane can be defined by two distinct lines, by three non-collinear points, or by one line and a point not on the line.

Plane geometry is the geometry of objects in 2 dimensional space.

Objects and planes

Two or more geometric objects are coplanar if there is a plane that contains all of them. Geometric objects are non-coplanar if there does not exist a plane that contains all of them.

A geometric object is planar if it can be entirely contained within one plane. A geometric object is non-planar if it can not be entirely contained within one plane.

Planes in 3-Space

Two planes in a 3-space either intersect or are parallel. If two planes are parallel, a line that is perpendicular to the one of the planes is also perpendicular to the other. If two planes intersect, the intersection forms a line. The angle between two intersecting planes is called a dihedral angle. If the dihedral angle between two planes is a right angle, then the planes are perpendicular.

Types of Planes

Planes are used in many contexts. Here are some of them.

Name	Illustration	Description
Cartesian Plane		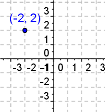A plane divided into four quadrants by two perpendicular number lines. The vertical number line represents a dependent variable and the horizontal number line represents the independent variable.
Rectangular coordinate plane
Complex Plane		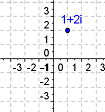A plane divided into four quadrants by two perpendicular number lines. Complex numbers can be plotted on a complex plane. The vertical number line represents the imaginary part of the complex number, and the horizontal number line represents the real part.
Argand diagram
Half-plane		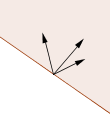A half-plane is a part of a plane cut off by a line.
Inclined plane	Click on the blue point and drag it to change the figure. Manipulative 1 - Perpendicular Planes Created with GeoGebra.	A plane that intersects a reference plane. The reference plane is usually horizontal.
Metric plane		Any two dimensional space which has a unit of measure for each dimension and a way to find the distance between any two points in the plane. Cartesian coordinates and Polar coordinates are examples of metric planes.
Table 1: Types of planes.

Postulates and Theorems of Planes

Some of the postulates and theorems dealing with planes are found in table 2. Click on the blue buttons in the manipulatives and drag them to change the figures.

Name	Manipulative	Description
Minimum Plane Postulate		A plane contains at least 3 non-collinear points.
Unique Plane Postulate		There is exactly one plane that passes through any 3 non-collinear points.
Same Plane Postulate		If two points lie in a plane, then the entire line joining those points lies in the same plane.
Intersecting Planes Postulate		If two planes intersect, then their intersection is a line.
Point, Line, Plane Theorem		If a point lies outside a line, then there is exactly one plane containing both the point and the line.
Intersecting Lines Plane Theorem		If two lines intersect, then there is exactly one plane containing both lines.
Table 2: Postulates and Theorems of Planes.

References

1. McAdams, David E.. All Math Words Dictionary, plane. 2nd Classroom edition 20150108-4799968. pg 139. Life is a Story Problem LLC. January 8, 2015. Buy the book

More Information

• McAdams, David E.. Coplanar. allmathwords.org. Life is a Story Problem LLC. 3/12/2009.
• Euclid of Alexandria. Elements. Clark University. 9/6/2018. https://mathcs.clarku.edu/~djoyce/elements/elements.html.

Cite this article as:

McAdams, David E. Plane. 3/26/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/p/plane.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/1/2018: Removed broken links, updated license, implemented new markup, updated geogebra app. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
1/6/2010: Added "References". (McAdams, David E.)
1/1/2010: Added information on plane geometry. (McAdams, David E.)
10/11/2008: Changed definition from '2-d surface' to '2-d space'. (McAdams, David E.)
4/30/2008: Added coplanar to more information. (McAdams, David E.)
2/26/2008: Added vocabulary hot links. (McAdams, David E.)
8/14/2007: Initial version. (McAdams, David E.)