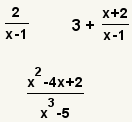Rational Expression
Pronunciation: /ˈræʃ.nl ɪkˈsprɛ.ʃən/ Explain
|
A rational expression is an expression that contains one or more ratios of polynomials. |
Simplifying Rational Expressions
Simplifying a rational expression is similar to reducing a fraction. Both simplifying a rational expression and reducing fractions involve finding common factors and canceling those factors.
Example 1
| Step | Equation | Description |
|---|---|---|
| 1 | 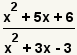 |
This is the rational expression to simplify. |
| 2 | 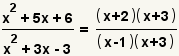 |
Factor both of the polynomials. |
| 3 | 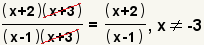 |
Cancel common factors and place any restrictions on the resulting expression. |
| Example 1 | ||
Example 2
| Step | Equation | Description |
|---|---|---|
| 1 | 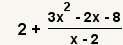 |
This is the rational expression to simplify. |
| 2 | 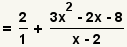 |
Transform the 2 to a fraction in order to find the common denominator. |
| 3 | 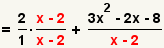 |
Multiply the 2 by ( x - 2 ) / ( x - 2 ) so the fractions can be combined. |
| 4 | 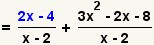 |
Multiply the first two fractions. |
| 5 | 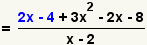 |
As the fractions now have a common denominator, combine the fractions. |
| 6 | 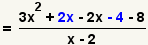 |
Use the commutative law of addition to put like terms next to each other. |
| 7 | 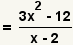 |
Combine like terms. |
| 8 | 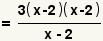 |
Factor the numerator and the denominator. |
| 9 | 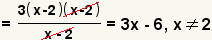 |
Cancel common factors and place any restrictions on the resulting expression. |
| Example 2 | ||
Addition and Subtraction of Rational Expressions
Two or more rational expressions can added or subtracted. Addition and subtraction of rational expressions is similar to addition and subtraction of fractions: The steps are:
- Find the least common denominator.
- Transform both rational expressions to the same common denominator.
- Add or subtract the rational expressions by adding or subtracting the numerators and using the least common denominator.
Example 3
| Step | Equation | Description |
|---|---|---|
| 1 | 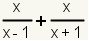 | This is the original expression. |
| 2 | The prime factorization of x - 1 is x - 1. | To find the common denominator, find the prime factorization of the denominator of the first expression. |
| 3 | The prime factorization of x + 1 is x + 1. | Find the prime factorization of the denominator of the second expression. |
| 4 | The factor x + 1 is not found in the
second denominator. The second rational expression will be multiplied by
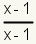 . . |
Identify the factors of the second denominator not in the first denominator. The first rational expression will be multiplied by a ratio of these factors. |
| 5 | 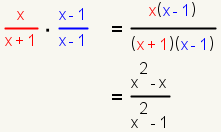 |
Multiply the first rational expression by the factors identified in step 4. |
| 6 | The factor x - 1 is not found in the
first denominator. The first rational expression will be multiplied by
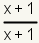 . . |
Identify the factors of the first denominator not in the second denominator. The second rational expression will be multiplied by a ratio of these factors. |
| 7 | 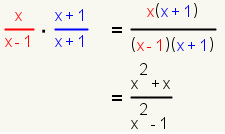 |
Multiply the second rational expression by the factors identified in step 6. |
| 8 | 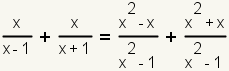 |
Transform the expressions using the multiplied rational expressions. |
| 9 | 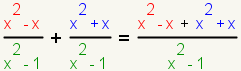 |
Add the numerators, and copy the denominator. |
| 10 | 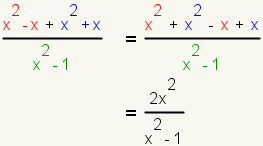 |
Simplify the numerator by combining like terms. |
| 11 | 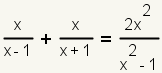 |
This is the answer. |
| Example 3 - Addition of rational expressions | ||
Example 4
| Step | Equation | Description |
|---|---|---|
| 1 | 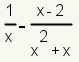 |
This is the original expression. |
| 2 | The prime factorization of x is x. | To find the common denominator, find the prime factorization of the denominator of the first expression. |
| 3 | The prime factorization of x2 + x is x( x + 1 ). | Find the prime factorization of the denominator of the second expression. |
| 4 | The factor x is found in the second denominator. The second rational expression is already common. | Identify the factors of the second denominator not in the first denominator. The first rational expression will be multiplied by a ratio of these factors. |
| 5 | The factor x is found in
the first denominator. The factor x + 1
is not found in the first denominator. The first rational expression
will be multiplied by 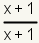 . . |
Identify the factors of the first denominator not in the second denominator. The second rational expression will be multiplied by a ratio of these factors. |
| 6 | 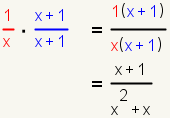 |
Multiply the second rational expression by the factors identified in step 6. |
| 7 | 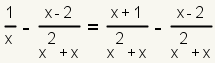 |
Transform the expressions using the multiplied rational expressions. |
| 8 | 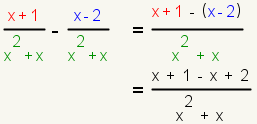 |
Add the numerators, and copy the denominator. |
| 9 | 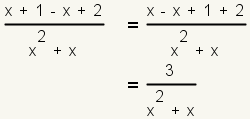 |
Simplify the numerator by combining like terms. |
| 10 | 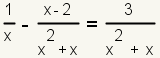 |
This is the answer. |
| Example 4 - Subtraction of rational expressions | ||
Multiplication and Division of Rational Expressions
Two or more rational expressions can multiplied. Multiplication and division of rational expressions is similar to multiplication and division of fractions: The steps are:
- Factor the rational expressions.
- Cancel common factors.
- Multiply the numerators.
- Multiply the denominators.
Example 5
| Step | Equation | Description |
|---|---|---|
| 1 | 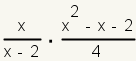 | This is the expression to multiply |
| 2 | 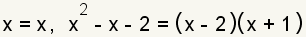 | Factor the numerators. This will allow you to more easily cancel common factors. |
| 3 | 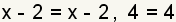 | Factor the denominators. This will allow you to more easily cancel common factors. |
| 4 | 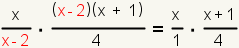 | Cancel common factors. |
| 5 | 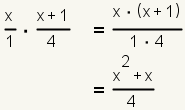 | Multiply the numerators and multiply the denominators. |
| 6 | 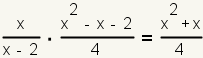 | This is the answer. |
| Example 5 - Multiplication of rational expressions | ||
To divide rational expressions, multiply the divided by the reciprocal of the divisor.
Example 6
| Step | Equation | Description |
|---|---|---|
| 1 | 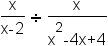 | This is the expression to divide. |
| 2 | 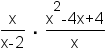 | Multiply by the reciprocal of the divisor. |
| 3 | 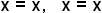 | Factor the numerators. This will allow you to more easily cancel common factors. |
| 4 | 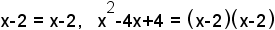 | Factor the denominators. This will allow you to more easily cancel common factors. |
| 5 | 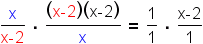 | Cancel common factors. |
| 6 | 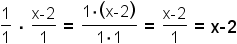 | Multiply the numerators and multiply the denominators. |
| 7 | 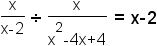 | This is the answer. |
| Example 6 - Division of rational expressions | ||
References
- McAdams, David E.. All Math Words Dictionary, rational expression. 2nd Classroom edition 20150108-4799968. pg 150. Life is a Story Problem LLC. January 8, 2015. Buy the book
Cite this article as:
McAdams, David E. Rational Expression. 4/30/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/r/rationalexpression.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/30/2019: Changed equations and expressions to new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/4/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
11/10/2009: Added addition, subtraction, multiplication and division of rational expressions. (McAdams, David E.)
1/20/2009: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License