Cometa
|
Una cometa es un cuadrilátero con dos sistemas de lados adyacentes, congruentes. Chasque encendido los puntos azules en el manipulante 1 y arrástrelos para cambiar la figura. Características de una cometa
|
Construcción del circunferencia inscrita de una cometa
| Paso | Diagrama | Descripción |
|---|---|---|
| 1 | 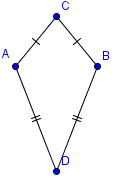 | Comience con una cometa convexa. |
| 2 | 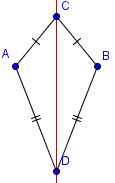 | Construya el bisectriz angular de uno de los ángulos que conectan lados congruentes. |
| 3 | 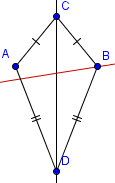 | Construya el bisectriz angular de uno de los ángulos que conectan lados no-congruentes. |
| 4 | 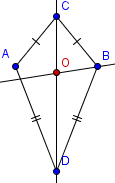 | Etiquete la intersección de bisectors de los pasos 2 y 3 como O. |
| 5 | 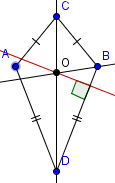 | Construya una recta a través de perpendicular de O a uno de los lados. |
| 6 | 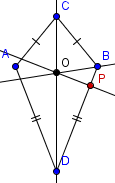 | Etiquete la intersección de la recta construida en el paso 5 con el lado a el cual es perpendicular como P. |
| 7 | 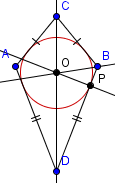 | Construya un circunferencia con el centro O y el radio OP. |
| Cuadro 1 | ||
Citar este artículo como:
Cometa. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/k/kite.html.
Traducciones
créditos de imagen
- Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisión
2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-12-13: Acoplamientos agregados del vocabulario, características de una cometa, y construcción del incircle de una cometa (McAdams, David.)
2008-09-16: Versión inicial (McAdams, David.)
- Navegación
- Home
- Contenido
-
# A B C D E F G H I J L M N O P Q R S T U V X Y - Ayudas del profesor
- Demostraciones de la Clase
- Referencia recíproca
- Geometría de NYSDE
- LIASP
- LIASP Home
- Condiciones del uso
- Política de aislamiento
- Done a LIASP
- Estructura de la ayuda este sitio
- Sobre LIASP
- LIASP del Contacto
Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de
Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
 Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
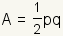 donde está la longitud p de uno diagonal y q es la longitud de la otra diagonal. Vea el manipulante 1.
donde está la longitud p de uno diagonal y q es la longitud de la otra diagonal. Vea el manipulante 1.