Arithmetic Precision

Pronunciation: /æ.rɪθˈmɛ.tɪk prɪˈsɪ.ʒən/ Explain

Arithmetic precision refers to the number of digits that are meaningful when expressing a value. In pure mathematics, the digits of a number can go on forever. In practical mathematics, computers can only handle a finite number of digits and measuring instruments can only measure a finite number of digits. The number of digits that are meaningful is the arithmetic precision. One says that there are 'n' significant digits.

Measurement and Arithmetic Precision Figure 1: A metric ruler being used to measure banana seeds. Measuring devices can only measure a finite number of digits. Figure 1 shows banana seeds being measured using a metric ruler. The smallest unit of measure on the ruler is millimeters. Each of the banana seeds measures approximately 16 millimeters. Since there are 2 digits in 16, the measurement is accurate to 2 significant digits. See also Measurement Error.

Computation and Arithmetic Precision

Computation is necessarily limited to a finite number of digits. To compute 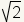, for example, to an infinite number of digits would take an infinite amount of memory and an infinite amount of time. So, when computing values, one chooses an arithmetic precision, or how accurate one wishes the computation to be. For computing devices that store numbers in binary format, such as most computers and many calculators, arithmetic precision is measured in binary digits. For computing devices that store numbers in decimal format, such as many calculators, arithmetic precision is measured in decimal digits.

References

1. McAdams, David E.. All Math Words Dictionary, arithmetic precision. 2nd Classroom edition 20150108-4799968. pg 20. Life is a Story Problem LLC. January 8, 2015. Buy the book

More Information

• Floating Point Arithmetic: Issues and Limitations. docs.python.org. The Python Tutorial. Python Software Foundation. 6/19/2018. https://docs.python.org/3/tutorial/floatingpoint.html.

Cite this article as:

McAdams, David E. Arithmetic Precision. 4/12/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/a/arithmeticprecision.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
• Metric ruler measuring banana seeds: Firetwister, http://commons.wikimedia.org. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license. https://commons.wikimedia.org/wiki/File:Banana_seeds.jpg.

Revision History

4/12/2019: Changed equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/15/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
3/19/2011: Added links to Measurement Error and Computational Error. (McAdams, David E.)
11/23/2009: Initial version. (McAdams, David E.)