Irrational Number
Pronunciation: /ɪˈræ.ʃə.nl ˈnʌm.bər/ ExplainAn irrational number is a real number that can not be expressed as the ratio of two integers. Since a rational number is a real number that can be expressed as the ratio of two integers, this means that any real number is either rational or irrational, but can not be both.
In math, one can
represent
numbers in ways that mask their true identity. For example, the square root
of 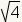 can be reduced to 2,
and so
can be reduced to 2,
and so 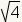 not an irrational number, even if it is represented by
using a square root.
not an irrational number, even if it is represented by
using a square root.
Examples of irrational numbers include π,
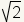 , and
, and
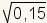 .
.
Here are some examples of numbers that are not irrational: 5.2,
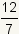 ,
3, and
,
3, and
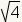 .
.
Properties of irrational numbers
| Property | Description |
|---|---|
| Continuity | The set of irrational numbers is not a continuous set. |
| Addition | Addition of irrational numbers is the same as addition of real numbers. |
| A, elements a, b of set A, and an operation * on set A, set A is closed with respect to * if and only if a * b is a member of set A. Click for more information.">Closure with respect to addition | The set of irrational numbers is not closed with respect to addition
since 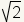 + - + -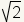 = 0.
0 is not an irrational number. = 0.
0 is not an irrational number. |
| Associative property of addition | The set of irrational numbers is associative with respect to addition. Since all irrational numbers are also real numbers, and the set of real numbers is associative with respect to addition, the associative property of addition applies to irrational numbers. |
| Additive identity | The additive identity for real numbers is zero. Zero is not in the set of irrational numbers. The set of irrational numbers does not have the property of identity with respect to addition. |
| Additive inverse | The additive inverse of an irrational number a is -a since a + (-a) = 0. The set of irrational numbers is invertible with respect to addition. |
| Group with respect to addition | Since the additive identity of irrational numbers is not itself an irrational number, the set of irrational numbers does not form a group with respect to addition. |
| Multiplication | Multiplication of irrational numbers is the same as multiplication of real numbers. |
| Closure with respect to multiplication | The set of irrational numbers is not closed with respect to
multiplication since 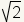 · ·
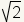 = 2. 2 is not an
irrational number. = 2. 2 is not an
irrational number. |
| Associative property of multiplication | The set of irrational numbers is associative with respect to multiplication. Since all irrational numbers are also real numbers, and the set of real numbers is associative with respect to multiplication, the associative property of multiplication applies to irrational numbers. |
| Multiplicative identity | The multiplicative identity for real numbers is one. One is not in the set of irrational numbers. The set of irrational numbers does not have the property of identity with respect to multiplication. |
| Multiplicative inverse | The multiplicative inverse of an irrational number a is 1 / a since a · 1/a = 1, a ≠ 0. The set of irrational numbers is invertible with respect to multiplication. |
| Group with respect to multiplication | Since the multiplicative identity of irrational numbers is not itself an irrational number, the set of irrational numbers does not form a group with respect to multiplication. |
| Cardinality | The cardinality of the irrational numbers is ℵ1 = 2ℵ0. The set of irrational numbers is uncountable. |
| Table 1: Properties of irrational numbers. | |
Proof of the existence of irrational numbers
The first proof of the existence of irrational numbers is attributed to a Pythagorean, a member of an ancient Greek religion. It proceeds as follows:
| Step | Equations/Diagrams | Discussion | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | Claim | Assume that the length of the hypotenuse and the length of the legs of an isosceles right triangle are both rational numbers. Since ratio of two rational numbers can be reduced to another rational number, there is a ratio of two integers c:b that can represent the ratio of any two rational numbers. | ||||||
| 2 | 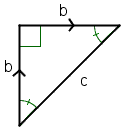 |
Let c:b be the ratio of lengths of the hypotenuse to a leg of a isosceles right triangle expressed in smallest terms where c and b are both integers. Since c:b is expressed in the smallest terms, c and b have no factors in common. | ||||||
| 3 |
|
Start with the Pythagorean theorem: A2 + B2 = C2. Then substitute the variables from the diagram in step 1. Substitute b in for A and B. Substitute c in for C. Then combine the like terms to get the equation 2b2 = c2. | ||||||
| 4 | 2b2 = c2 | The definition of an even number is a number that has 2 as a factor. Since c2 = 2b2, 2 is a factor of c2. This means that c2 is an even number. | ||||||
| 5 | c is even. | Since c2 has a factor of 2 and c2 = c · c, c must also have a factor of 2. So c is even. | ||||||
| 6 | b is odd. | Since c:b is in the lowest terms, b has no factors in common with c. So b can not have a factor of 2. This means that b must be odd. | ||||||
| 7 | c = 2y | Since c is even, there is an integer y such that c = 2y. | ||||||
| 8 | 4y2 = 2b2 | Since c2 = 2b2, substitute 2y in for c. This gives the equation (2y)2 = 2b2. Expand the exponent on the left side of the equation to get 4y2 = 2b2. | ||||||
| 9 | 2y2 = b2 | Take the equation 4y2 = 2b2 and simplify. This gives the equation 2y2 = b2. | ||||||
| 10 | b is even. | By a similar argument to steps 3 and 4, b must be even. | ||||||
| 11 | Contradiction | Since b can not be both even and odd, a contradiction exists. This means that the measures of both the leg and the hypotenuse of a isosceles right triangle can not be rational numbers. So a number that is not a rational number must exist. | ||||||
| Table 2: Proof of the existence of irrational numbers. | ||||||||
References
- McAdams, David E.. All Math Words Dictionary, irrational number. 2nd Classroom edition 20150108-4799968. pg 103. Life is a Story Problem LLC. January 8, 2015. Buy the book
Cite this article as:
McAdams, David E. Irrational Number. 4/23/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/i/irrational.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/23/2019: Updated equations and expressions to new format. (McAdams, David E.)3/22/2019: Corrected mulitplicative inverse. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
8/28/2018: Corrected spelling. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
8/6/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
3/3/2010: Added "References", added section on the proof of existence of irrational numbers. (McAdams, David E.)
8/13/2008: Changed some math constructs to images. Added understanding check (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License