Notation

Pronunciation: /noʊˈteɪ.ʃən/ Explain

Notation is a way to write something down using special signs or symbols. In mathematics, notation is used a lot. Mathematical notation allows one to express a mathematical idea in a shorter and much more easily understood format than plain English. The examples in table 1 show why this is true.

Notation	Example	Meaning
Decimal Numbers	34.7	Decimal numbers are a notation for expressing numbers using base 10.
Scientific Notation	3.753 × 1023	Scientific notation is used to express very large or very small numbers in base 10 without using a lot of zeros. The number expressed in scientific notation could be written in decimal notation as 375,300,000,000,000,000,000,000.
Algebraic notation	y = 3x2 + 4	A sentence that could be used to mean the same thing as the equation is: "Let y be equal to three times the value of x squared plus 4." However, in this sentence it is not clear whether one multiplies three times x first or squares x first. The algebraic order of operations tells us what has to be done first in the equation.
Probability function	P(A) = 0.5	A sentence that could be used to mean the same thing as the equation is: "The probability of event A happening is 0.5.
Table 1: Examples of Mathematical Notation.

Summary of Mathematical Notation

Notation	Description
Numbers
14	integer
1.5	real number
3+4i	complex number
2.2i	imaginary number
7/15	rational number, fraction
∞	infinity
–	negative
+	positive
%	percent
3.77×104	scientific notation
2.64E05	E notation
a < b	a is less than b
a ≤ b	a is less than or equal to b
a = b	a is equal to b
a ≠ b	a is not equal to b
a ≥ b	a is greater than or equal to b
a > b	a is greater than b
x | y	x divides y
x ≡ y mod. q	x is congruent with y modulo q
z = a + bi	complex number
a + bi = a - bi	complex conjugate
ℑ, Im	imaginary part of a complex number
ℜ, Re	real part of a complex number
Sets of Numbers
[m, n]	closed interval from m to n
(m, n), ]m, n[	open interval from m to n
(m, n], ]m, n]	half open interval on the left from m to n
[m, n), [m, n[	half open interval on the right from m to n
(-8, 8)	interval of all real numbers
…	ellipsis
sup.	supremum
inf.	Infimum
Arithmetic
a + b	addition, add a to b
a – b	subtraction; subtract b from a
-b	negation; negative b
a ± b	a plus or minus b
a × b	multiply a by b
a · b	multiply a by b
ab	multiply a by b
a * b	multiply a by b in some computer languages.
ab	exponentiation: a raised to the b power; a multiplied times itself b times.
a ^ b	exponentiation in some computer languages
a ** b	exponentiation in some computer languages.
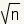	square root of n
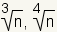	cube root of n, fourth root of n, etc.
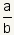	fraction, division
a ÷ b	a divided by b
a / b	a divided by b
a : b	ratio of a to b, divided by
a * b	an arbitrary operator
a…z, A…Z	variables
a1, a2, a3, …	indexed variables
a ≡ b	a is identical to, is equivalent to b
c = a mod. b	c is congruent to a modulo b.
→	approaches, implies
⇒	implies
a ∝ b	a varies as b, a is proportional to b.
∞	infinity
f ∘ g(x)	composition of functions
( )	parenthesis, grouping of operations
[ ]	brackets, grouping of operations
{ }	braces, grouping of operations, see also sets
nº	n degrees
n'	n minutes (1/60th degree)
n'	n feet.
n"	n seconds (1/60th minute)
Δx	change in x, delta x
∑	sum of a sequence
f(x)	function of x
n!	n factorial
|x|	absolute value of x, magnitude of x
⌈ x ⌉	ceiling function of x
⌊ x ⌋	floor function of x
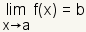	the limit of f(x) as x approaches a is equal to b.
Geometry
≅	is congruent with
≇	is not congruent with
~	is similar to
AB	line segment AB
AB	length of line segment AB
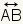	line AB
AB	ray AB
∠α	angle alpha
m∠α	the measure of angle alpha
ΔABC	triangle ABC
l ∥ m	l is parallel to m
l ∦ m	l is not parallel to m
l ⊥ m	l is perpendicular to m
	minor arc with endpoints J and K
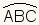	major arc containing point B
P, Q	propositions
¬P, ~P	negation, NOT P
P ∨ Q, P + Q	disjunction
P ∧ Q, P · Q	conjunction, P AND Q
P ⊕ Q	exclusive disjunction, P xor Q
P → Q	P implies Q
P ⇒ Q	P implies Q
P ↔ Q	equivalence, biconditional
P ≡ Q	equivalence
P = Q	equivalence
≡	identity
0, F	false
1, T	true
∴	therefore, in conclusion
Q.E.D.	End of proof
Set Theory
A, B, C, …	set
a, b, c, …	member of a set
a ∈ A	a is a member of A
a ∉ A	a is not a member of A
A ⊂ B	A is a subset of B
A ⊆ B	A is a subset of or equal to B
B ⊃ A	B is a superset of A
A ⊄ B	A is not a subset of B
A ⊈ B	A is neither a subset of or equal to B
A ∪ B, A + B	A union B
A ∩ B, A · B	A intersection B
A – B	difference of A and B.
∅, { }	empty set, null set
A'	complement of set A
A / S	complement of set A in S.
{ x: P(x)}	the set of all x with property P
{ a, b, c, …}	set
( a, b, c, …)	ordered set
< a, b, c, … >	ordered set
A × B	Cartesian product A cross B
f ∘ g(x)	composite function
f(X)	image of set X
one to one	one to one correspondence
|X|	cardinality of set X
ℵ0	denumerable infinity
ℵ1, ℵ1, ℵ2	nondenumerable infinities
P(A)	power set of A
Probability
P(e)	probability of event e
P( e1, e2 )	conditional probability of e1 given e2.
E( X )	expectation of X
E( X, c )	conditional expectation of X, given condition c
e'	complement of event e.
Table 2: Summary of mathematics notation

References

1. McAdams, David E.. All Math Words Dictionary, notation. 2nd Classroom edition 20150108-4799968. pg 126. Life is a Story Problem LLC. January 8, 2015. Buy the book

Cite this article as:

McAdams, David E. Notation. 4/26/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/n/notation.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/26/2019: Changed equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
9/5/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
12/21/2009: Change More Information to Reference. (McAdams, David E.)
4/14/2008: Initial version. (McAdams, David E.)