Arithmetic Sequence
Pronunciation: /æ.rɪθˈmɛ.tɪk ˈsi.kwəns/ ExplainAn arithmetic sequence is a finite sequence of numbers with a common difference.[2] For example, the arithmetic sequence { 1, 3, 5, 7 } has a common difference of 2 since 1 + 2 = 3, 3 + 2 = 5 and 5 + 2 = 7.
Notation for Arithmetic Sequence
Arithmetic sequence can be denoted {a0 + k · d}k=0..n-1 where:
- a0 is the value of the first term;
- d is the common difference; and
- n is the number of terms in the sequence.
Take the arithmetic sequence { 1, 3, 5, 7 }. Since the first term is 1, a0 = 1. The common difference is 3 - 1 = 2, so d = 2. There are 4 terms in the sequence, so n = 4. This gives the expression { 1 + 2k }k=0..3.
Discovery
| Step | Example | Directions |
|---|---|---|
| 1 |  | Take a piece of paper. |
| 2 |  | Using a ruler, make tick marks along opposite edges. |
| 3 |  | Using a straightedge, connect the tick marks. |
| 4 | 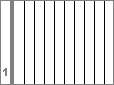 | Using scissors, cut off one of the strips. How many strips do you have so far? Write it like this { 1 }. |
| 5 |  | Cut off another strip of paper. How many strips do you have now? Write it like this { 1, 2 }. |
| 6 |  | Continue cutting off strips until the paper is completely cut. Write down the sequence. |
| 7 | (1 + k)k=0..3 | Now write the sequence using arithmetic sequence notation. |
Understanding Check
Write down your answer to the following questions. Then click on the 'answer' icon to see if you understand.
| Item | Arithmetic Sequence | First Term | Common Difference | Number of Terms | Expression |
|---|---|---|---|---|---|
| 1 | { 4, 7, 10, 13, 16 } | Click for Answer 4
| Click for Answer 3
| Click for Answer 5
| Click for Answer {4 + 3·k}k=0..4
|
| 2 | { -1, 1, 3, 5, 7, 9 } | Click for Answer -1
| Click for Answer 2
| Click for Answer 6
| Click for Answer {-1 + 2·k}k=0..5
|
| 3 | Click for Answer { 6, 8, 10, 12 }
| Click for Answer 6
| Click for Answer 2
| Click for Answer 4
| { 6 + 2·k }k=0..3 |
| 4 | Click for Answer { 9, 6, 3, 0, -3 }
| Click for Answer 9
| Click for Answer -3
| Click for Answer 5
| { 9 - 3·k }k=0..4 |
References
- McAdams, David E.. All Math Words Dictionary, arithmetic sequence. 2nd Classroom edition 20150108-4799968. pg 20. Life is a Story Problem LLC. January 8, 2015. Buy the book
- arithmetic progression. merriam-webster.com. Encyclopedia Britannica. Merriam-Webster. Last Accessed 6/12/2018. https://www.merriam-webster.com/dictionary/arithmetic%20progression. Buy the book
- Bettinger, Alvin K. and Englund, John A.. Algebra and Trigonometry. pp 260-262. www.archive.org. International Textbook Company. January 1963. Last Accessed 6/12/2018. http://www.archive.org/stream/algebraandtrigon033520mbp#page/n277/mode/1up/search/progression. Buy the book
- Jones, Burton. Elementary Concepts of Mathematics. pp 118-122. www.archive.org. MacMillan and Company. 1947. Last Accessed 6/12/2018. http://www.archive.org/stream/elementaryconcep029487mbp#page/n138/mode/1up. Buy the book
Cite this article as:
McAdams, David E. Arithmetic Sequence. 4/12/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/a/arithmeticsequence.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/12/2019: Changed equations and expressions to new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/15/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
1/6/2010: Added "References". (McAdams, David E.)
4/5/2008: Adding discovery activity. (McAdams, David E.)
2/3/2008: Added color to example of common difference. (McAdams, David E.)
8/7/2007: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License