Associative Property of Multiplication

Pronunciation: /əˈsoʊ.siˌeɪ.tɪv ˈprɒp.ər.ti ʌv ˌmʌl.tə.plɪˈkeɪ.ʃən/ Explain

The associative property of multiplication states that, when multiplying three numbers, it does not matter in which order they are multiplied.^[2] This is expressed by the equation: a·(b·c) = (a·b)·c.

One way to remember the associative property of multiplication is to use the root word, 'associate'. So in the associative property of multiplication, the variables b and c associate closely on one side of the equals, while a and b associate closely on the other side.

A representation of the associative property of multiplication using dots is:

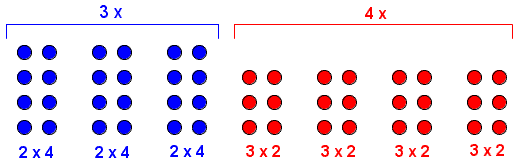Figure 1: 3·(2·4) = (3·2)·4 = 24.

References

1. McAdams, David E.. All Math Words Dictionary, associative property of multiplication. 2nd Classroom edition 20150108-4799968. pg 21. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. Fine, Henry B., Ph. D.. Number-System of Algebra Treated Theoretically and Historically. 2nd edition. pg 5. www.archive.org. D. C. Heath & Co., Boston, U.S.A.. 1907. Last Accessed 6/12/2018. http://www.archive.org/stream/thenumbersystemo17920gut/17920-pdf#page/n14/mode/1up/search/associative. Buy the book
3. Bettinger, Alvin K. and Englund, John A.. Algebra and Trigonometry. pg 2. www.archive.org. International Textbook Company. January 1963. Last Accessed 6/12/2018. http://www.archive.org/stream/algebraandtrigon033520mbp#page/n18/mode/1up. Buy the book

More Information

• McAdams, David E.. Associative. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 6/19/2018. https://www.allmathwords.org/en/a/associative.html.

Cite this article as:

McAdams, David E. Associative Property of Multiplication. 4/12/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/a/associativemultiplication.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/12/2019: Changed equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/15/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
12/19/2009: Added "References". (McAdams, David E.)
6/24/2008: Added caption to figure 1. (McAdams, David E.)
6/16/2008: Initial version. (McAdams, David E.)