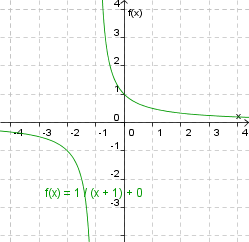
Asymptote
Pronunciation: /ˈæ.sɪmˌtoʊt/ Explain
|
An asymptote is a
linear
boundary that a curve gets very close to, but never reaches.[2]
Figure 1 is the graph of the function
|
 Understanding Check
Understanding Check
|
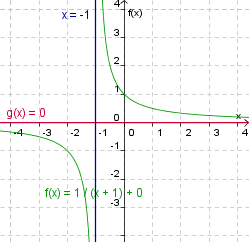
Figure 2 is a graph of the function Click here to see the answer.
The asymptotes of
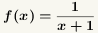 are x = -1
and f(x) = 0. are x = -1
and f(x) = 0.
|
Discovery
|
Click on the points on the slider bars to change the figure. As you slide the bars, the equation for the function changes. This also changes the asymptotes. What is the relationship between the function and the asymptotes? |
| Manipulative 1 - Asymptote Created with GeoGebra. |
References
- McAdams, David E.. All Math Words Dictionary, asymptote. 2nd Classroom edition 20150108-4799968. pg 22. Life is a Story Problem LLC. January 8, 2015. Buy the book
- Hustler, James Devereux. The Elements of the Conic Sections with the Sections of the Conoids. 3rd edition. pg 43. www.archive.org. Published by J. Deighton and Sons. 1826. Last Accessed 6/12/2018. http://www.archive.org/stream/elementsofconics00hastuoft#page/43/mode/1up/search/asymptote. Buy the book
Cite this article as:
McAdams, David E. Asymptote. 4/12/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/a/asymptote.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/12/2019: Changed equations and expressions to new format. (McAdams, David E.)1/11/2019: Changed text to match illustration. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/15/2018: Removed broken links, changed Geogebra links to work with Geogebra 5, updated license, implemented new markup. (McAdams, David E.)
1/7/2010: Added "References". (McAdams, David E.)
10/6/2008: Changed understanding check so image changes on click for answer. (McAdams, David E.)
6/25/2008: Added understanding check and discovery. (McAdams, David E.)
3/25/2008: Replaced graphic in figure 1. (McAdams, David E.)
7/25/2007: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License
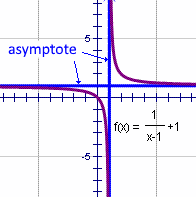
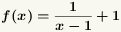 .
The vertical asymptote is the line
.
The vertical asymptote is the line