Complete the Square
Pronunciation: /kəmˈplit ðə skwɛər/ ExplainComplete the square is an algorithm used to convert a quadratic equation into vertex form.[2] The complete the square algorithm is also used to derive the quadratic equation. Table 1 gives the algorithm for completing the square.
| Step | Quadratic Equation | Vertex Form | Description |
|---|---|---|---|
| 1 | 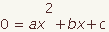 | Start with the equation in standard form. | |
| 2 | 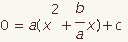 | 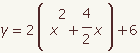 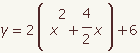 | Use the distributive property of multiplication of addition and subtraction to get x2 + bx inside parenthesis. |
| 3 | 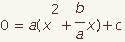 | 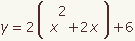 | Simplify, if possible. |
| 4 | 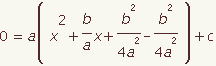 | 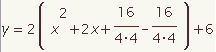 | Add and subtract b2 / (4a2). |
| 5 | 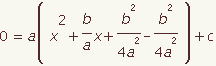 | 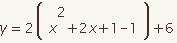 | Simplify, if possible. |
| 6 | 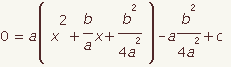 | 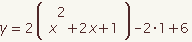 | Use the distributive property of multiplication over addition and subtraction to move -(b / 2a)2 out of the parenthesis. |
| 7 | 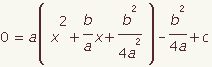 | 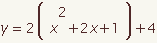 | Simplify if possible. |
| 8 | 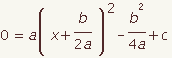 | 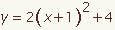 | Factor the square. |
| 9 | 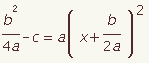 | 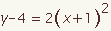 | Subtract the constant term from both sides. The equation is now in vertex form. This demonstration will continue to derive the quadratic formula by solving for x. |
| 10 | 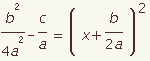 |  | Divide both sides by a. |
| 11 | 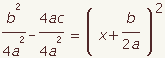 |  | Make 4a2 the common denominator. |
| 12 | 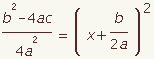 |  | Combine the fractions. |
| 13 | 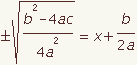 |  | Take the square root of both sides. |
| 14 | 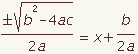 |  | Simplify. |
| 15 |  |  | Subtract b / (2a) from both sides. |
| 16 | 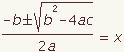 |  | Combine the fractions. |
| 17 | 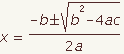 |  | Use the symmetric property of equality to put the x on the left of the equals sign. This is the quadratic formula. |
| Table 1: The complete the square algorithm | |||
Geometric Interpretation of Complete the Square
| Step | Diagram | Description |
|---|---|---|
| 1 | 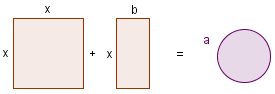 | The square has dimensions x by x so the square represents x2. The rectangle has dimensions b by x, so the rectangle represents bx. The circle represents a. |
| 2 | 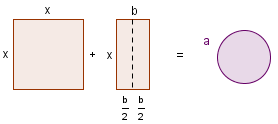 | The rectangle can be divided in half. Each half represents bx / 2. |
| 3 | 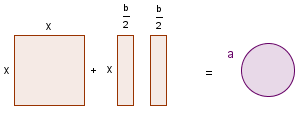 |  |
| 4 | 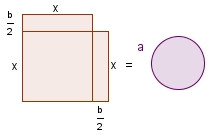 | Move the two rectangles around the square to form part of a larger square. |
| 5 | 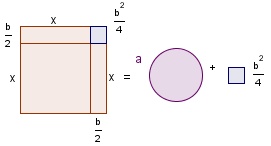 | Complete the square by adding b2/4 to both sides. |
| Table 2: Geometric interpretation of complete the square. | ||
References
- McAdams, David E.. All Math Words Dictionary, complete the square. 2nd Classroom edition 20150108-4799968. pg 39. Life is a Story Problem LLC. January 8, 2015. Buy the book
- Wells, Webster. A Complete Course in Algebra for Academies and High Schools. pp 213-217. www.archive.org. Wells' Mathematical Series. Leach, Shewell & Sandborn. 1885. Last Accessed 6/25/2018. http://www.archive.org/stream/courseincomplete00wellrich#page/213/mode/1up/search/square. Buy the book
- Bettinger, Alvin K. and Englund, John A.. Algebra and Trigonometry. pp 206-209. www.archive.org. International Textbook Company. January 1963. Last Accessed 6/25/2018. http://www.archive.org/stream/algebraandtrigon033520mbp#page/n223/mode/1up. Buy the book
More Information
- McAdams, David E.. Vertex Form. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 6/27/2018. https://www.allmathwords.org/en/v/vertexform.html.
Cite this article as:
McAdams, David E. Complete the Square. 4/14/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/c/completethesquare.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/14/2019: Updated equations and expressions to new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/25/2018: Removed broken links, updated license, implemented new markup, updated GeoGebra apps. (McAdams, David E.)
1/17/2010: Added "References". (McAdams, David E.)
11/25/2008: Changed equations to images. (McAdams, David E.)
10/17/2008: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License