Difference Quotient

Pronunciation: /ˈdɪ.frəns ˈkwoʊ.ʃənt/ Explain

Click on the blue points and drag them to change the figure. Where on the graph does the difference quotient approach zero? Manipulative 1 - Difference Quotient Created with GeoGebra.

The difference quotient is the slope of a secant line through two points of a curve.[2] 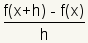In the difference equation, h is the change in x and f(x + h) - f(x) is the change in f(x) given the change in h. The difference quotient is used in calculus. As the two points grow closer together, the closer the slope of the secant line is to the slope of the curve. This gives the expression at the base of calculus: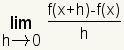

References

1. McAdams, David E.. All Math Words Dictionary, difference quotient. 2nd Classroom edition 20150108-4799968. pg 60. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. Smith, William Benjamin. Infinitesimal Analysis, Volume 1. pp 9-10. www.archive.org. The Macmillan Company. 1898. Last Accessed 7/3/2018. http://www.archive.org/stream/infinitsimalanly01willrich#page/n32/mode/1up/search/difference+quotient. Buy the book
3. Kuratowski, Kazimierz. Introduction To Calculus. U.S.A. edition. pp 138-140. Translated by Msielak, Julian. www.archive.org. Addison-Wesley Publishing Company Inc.. 1962. Last Accessed 7/3/2018. http://www.archive.org/stream/introductiontoca033502mbp#page/n143/mode/1up/search/difference+quotient. Buy the book

More Information

• How to Connect Slopes and Derivatives (video). dummies.com. Wiley. 1/23/2010. http://www.dummies.com/how-to/content/how-to-connect-slopes-and-derivatives.html.

Cite this article as:

McAdams, David E. Difference Quotient. 4/20/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/d/differencequotient.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/20/2019: Updated equations and expressions to the new format (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/4/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
1/23/2010: Added "References". (McAdams, David E.)
12/5/2008: Initial version. (McAdams, David E.)