Division
Pronunciation: /dɪˈvɪ.ʒən/ Explain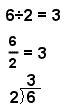
|
| Figure 1: Three ways to write the division problem 6 ÷ 2 = 3. |
Division is defined as the inverse of multiplication: a ÷ b = c if and only if a = b · c, b ≠ 0. Division can also be considered a shortcut for repeated subtraction. For example, 6 ÷ 2 means subtract 2 from 6 until less than 2 is left. (6 ÷ 2: 6 - 2 - 2 - 2 = 0, 2 is subtracted 3 times, so 6 ÷ 2 = 3).
The parts of division are the dividend, the divisor, and the quotient. dividend ÷ divisor = quotient The dividend is the value that is divided into. The divisor is the value that divided the dividend. The quotient is the result of the division.
Division of integers is often represented by rows of dots. For example, one can represent 6 ÷ 2 with 6 dots arranged in 2 columns.

|
| Figure 2: Representation of 2·3 |
Notation
Division is denoted in one of three ways:
| Form | Equation | Example |
|---|---|---|
| Operator form | 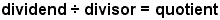 | 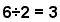
|
| Fraction form | 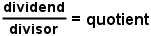 | 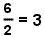
|
| Long division form | 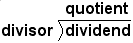 | 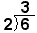
|
| Table 3: Division notation | ||
Property of Dividing by 1
Any number divided by 1 remains unchanged. To demonstrate this, use the definition of division, a ÷ 1 = c if and only if a = 1·c. But, apply the property of multiplying by 1 to get 1·c = c. Substituting c for 1·c, the equation becomes a = c. Substitute these values into the original definition of division: a ÷ 1 = a.
Division by zero
Division by zero is undefined. Division by zero has no mathematical meaning. See Division by 0 for more information.
How to use Algebra Tiles to Represent Division
Algebra tiles can be used to represent division of integers. Take the division problem 15 ÷ 5 = 3. Table 1 shows how to use algebra tiles to represent this problem. Follow the instructions on the left while dragging the tiles in the manipulative on the right. When you get done, the manipulative should look similar to the last image in this table.
| Step | Image | Description | Manipulative |
|---|---|---|---|
| 1 | 
| Start by counting out the number of tiles in the dividend. In the problem 15 ÷ 5, 15 is the dividend. | |
| 2 | 
| Now build columns of tiles. Each column will have the same number of tiles as the divisor. In the problem 15 ÷ 5, 5 is the divisor. | |
| 3 | 
| The second column also gets five tiles. | |
| 4 | 
| The third column also gets five tiles. All the tiles are used up. There are three rows, so 15 ÷ 5 = 3. | |
| Table 4: Algebra Tiles Example 1 | |||
Example 2
This example shows how to use algebra tiles to represent the division problem 14 ÷ 3.
| Step | Image | Description | Manipulative |
|---|---|---|---|
| 1 | 
| Start by counting out the number of tiles in the dividend. In the problem 14 ÷ 3, 14 is the dividend. | |
| 2 | 
| Now build columns of tiles. Each column will have the same number of tiles as the divisor. In the problem 14 ÷ 3, 3 is the divisor. | |
| 3 | 
| The second column also gets five tiles. | |
| 4 | 
| The third and forth columns also get three tiles. There are two tiles left over. There are four columns of three tiles plus two tiles left over, so 14 ÷ 3 = 4 remainder 2. | |
| Table 5: Algebra Tiles Example 2 | |||
References
- McAdams, David E.. All Math Words Dictionary, division. 2nd Classroom edition 20150108-4799968. pg 65. Life is a Story Problem LLC. January 8, 2015. Buy the book
Cite this article as:
McAdams, David E. Division. 4/20/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/d/division.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/20/2019: Updated equations and expressions to the new format (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/4/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
11/6/2011: Added links to "Division by 0". (McAdams, David E.)
5/5/2011: Initial version. (McAdams, David E.)
1/24/2010: Added "References". (McAdams, David E.)
11/28/2009: Authored. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License