Existence Theorem
Pronunciation: /ɪgˈzɪs.təns ˈθɪər.əm/ Explain|
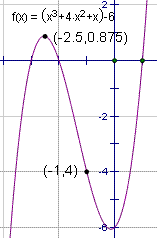
An existence theorem is a theorem that proves the existence of an entity or entities without telling how many entities there are or how to find them.[2] One example of an existence theorem is that for all continuous polynomials, if a value of the polynomial is positive for one value of x, and negative for another value of x, then the value of the polynomial must be zero somewhere in between the two values of x. In figure 1, the points (-2.5, 0.875) and (-1, -4) are plotted. Since f(-2.5) is positive, and f(-1) is negative, then for some value of x, -2.5 < x < -1, f(x) = 0. Notice that this theorem does not tell is for how many values of x that f(x) is zero, nor how to find the value of f(x). |
|
References
- McAdams, David E.. All Math Words Dictionary, existence theorem. 2nd Classroom edition 20150108-4799968. pg 75. Life is a Story Problem LLC. January 8, 2015. Buy the book
- Cupillari, Antonella. Nuts and Bolts of Proof: An Introduction to Mathematical Proofs. 3rd edition. pp 58-60. Academic Press. August 15, 2005. Last Accessed 7/9/2018. Buy the book
- Daniel J. Velleman. How to Prove It: A Structured Approach. 2nd edition. pp 146-153. Cambridge University Press. January 16, 2006. Last Accessed 7/9/2018. Buy the book
Cite this article as:
McAdams, David E. Existence Theorem. 4/20/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/e/existencetheorem.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/20/2019: Updated expressions and equations to match new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/5/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
2/2/2010: Added "References". (McAdams, David E.)
1/4/2009: Expanded 'More Information'. (McAdams, David E.)
6/10/2008: Initial version. (McAdams, David E.)
6/7/2008: Corrected spelling. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License