Expected Value

Pronunciation: /ɪkˈspɛkt.ɛd ˈvæl.ju/ Explain

In probability, an expected value is the probability of each and every event in a sample space times the probability that the event will occur.^[2] Since the expected value is numeric, the outcomes of the experiment must also be numeric. For experiments with finite outcomes, this can be calculated as the sum of the values of each outcome times the probability of that outcome occurring.

Example 1: Role of one die

Table 1 shows the outcomes and their probabilities for the roll of one fair die.

Outcome of roll	Probability	Outcome × Probability
1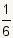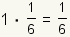
2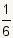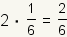
3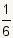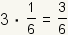
4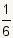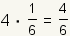
5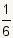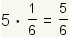
6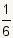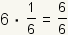
Table 1: Expected value of role of one fair die

So, the expected value is .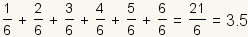

Example 2: Roll of two dice

Table 2 shows the outcomes and their probabilities for the roll of two fair dice.

Outcome of roll	Probability	Outcome × Probability
2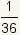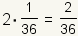
3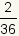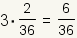
4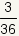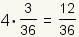
5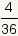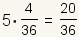
6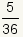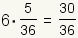
7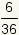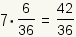
8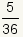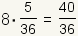
9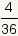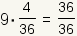
10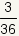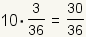
11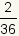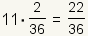
12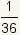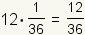
Table 2: Expected value of role of two fair dice

So, the expected value is .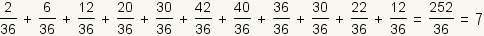

References

1. McAdams, David E.. All Math Words Dictionary, expected value. 2nd Classroom edition 20150108-4799968. pg 75. Life is a Story Problem LLC. January 8, 2015. Buy the book

Cite this article as:

McAdams, David E. Expected Value. 12/21/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/e/expectedvalue.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/18/2018: Changed title to common format. (McAdams, David E.)
7/5/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
2/2/2010: Added "References". (McAdams, David E.)
12/1/2009: Initial version. (McAdams, David E.)