Harmonic Series
Pronunciation: /hɑrˈmɒn.ɪk ˈsɪər.iz/ ExplainA harmonic series is the series of numbers
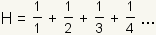 .
The harmonic series is important because it lies between series that
converge
and series that
diverge.
The harmonic series is divergent. This is especially interesting in light of the fact that the sequence of terms converges to zero.
The harmonic sequence is the sequence
.
The harmonic series is important because it lies between series that
converge
and series that
diverge.
The harmonic series is divergent. This is especially interesting in light of the fact that the sequence of terms converges to zero.
The harmonic sequence is the sequence
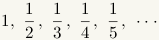 .
The harmonic sequence is convergent, but the harmonic series is divergent.
.
The harmonic sequence is convergent, but the harmonic series is divergent.
The harmonic series is so named because it contains the overtones of a vibrating strings. If a string vibrates at a particular frequency, The first overtone has a frequency of 1/2 of the original, the second 1/3, and so on.
The divergence of the harmonic series was first proved in the 14th century by Nicole Oresme. Nicole Oresme used a comparison proof. A modern rendition of this proof is as follows:
Let H denote the harmonic series.
Group the terms of H as follows:Define a new series I (which will be easier to analyze by replacing each term in a bracketed grouping by the smallest term in that grouping.Clearly H is not less than the new series I, as the sum of terms in each bracketed grouping of H is not less than the sum of terms for the corresponding grouping of I.Observe that
which diverges.
is the same as
But H is not less than I, so H also diverges.
Alternating harmonic series
The alternating harmonic series is the series
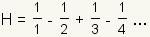 .
The alternating harmonic series is convergent. This can be shown
using the alternating series test.
.
The alternating harmonic series is convergent. This can be shown
using the alternating series test.
References
- McAdams, David E.. All Math Words Dictionary, harmonic series. 2nd Classroom edition 20150108-4799968. pg 89. Life is a Story Problem LLC. January 8, 2015. Buy the book
Cite this article as:
McAdams, David E. Harmonic Series. 3/16/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/h/harmonicseries.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)7/16/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
1/3/2011: Added external reference to harmonic sequence. (McAdams, David E.)
10/25/2010: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License
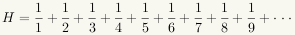
![H = 1/1 + [1/2] + [1/3 + 1/4] + [1/5 + 1/6 + 1/7 + 1/8] + [1/9 + ...](../../equations/h/harmonicseries03.png)
![I = 1/1 + [1/2] + [1/4 + 1/4] + [1/8 + 1/8 + 1/8 + 1/8] + [1/16 + ...](../../equations/h/harmonicseries04.png)
![I = 1/1 + [1/2] + [2/4] + [4/8] + [8/16] + ...](../../equations/h/harmonicseries05.png)
![I = 1/1 + [1/2] + [1/2] + [1/2] + [1/2] + ...](../../equations/h/harmonicseries06.png)