How to Inscribe a Circle in a Triangle

Click on the blue points and drag them to change the figure.

Can the incenter (point D) be outside the triangle? How do you know.
Manipulative 1 - Inscribed Triangle Created with GeoGebra.
StepExampleDescription
1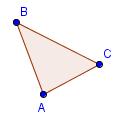Triangle ABC Start with triangle ABC.
2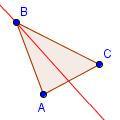Triangle ABC with angle bisector for angle ABC. Draw the angle bisector of angle ABC.
3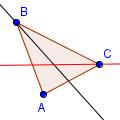Triangle ABC with angle bisector for angle BCA. Draw the angle bisector of angle BCA. For steps 2 and 3, any two angles can be bisected.
4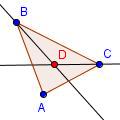Triangle ABC with point D at the intersection of the two angle bisectors. Draw point D at the intersection of the angle bisectors.
5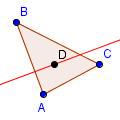Triangle ABC with a line through point D perpendicular to side AB. Draw a line through point D perpendicular to side AB. Note that this line can be perpendicular to any of the sides.
6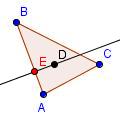Triangle ABC with point E at intersection of perpendicular line and side AB. Mark point E at the intersection of the perpendicular and side AB.
7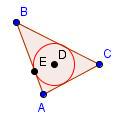Triangle ABC with circle centered at D with a radius of DE. Draw a circle with center at D with a radius of DE.

Check Mark Understanding Check

Use the GeoGebra application below to construct the circumscribing circle about the rectangle.

Click on the blue points and drag them to change the figure.
Manipulative 2 - How to inscribe a circle in a triangle using Geogebra Created with GeoGebra.
  1. Click on the down arrow of the construction GeoGebra construction button. to open the construction menu. Select the Angle Bisector GeoGebra angle bisector menu button. menu item. Then click on points B, A, then C. You have constructed the angle bisector of angle BAC.
  2. Now click on point A, B, then C. You have constructed the angle bisector of angle ABC.
  3. Click on the down arrow of the Point menu button Geogebra point menu button.. Select the Intersect Two Objects Geogebra intersect two objects menu button menu button. Click on each of the two angle bisectors. Point D that appears at the intersection of the two angle bisectors is the incenter.
  4. Click on the arrow in the angle bisector menu button GeoGebra angle bisector menu button. to open the construction menu. Click on the perpendicular line menu button GeoGebra perpendicular line menu button.. Now click on the incenter (point C) then one side of the triangle. The point where the perpendicular line intersects the side of the triangle is on the incircle.
  5. Click on the Intersect Two Objects Geogebra intersect two objects menu button button, then click on the perpendicular line, and the side to which it is perpendicular. Point E appears. Point E is on the incircle.
  6. Click on the Circle With Center Through Point GeoGebra circle with center through two points menu button.. Then click on the incenter (point D) then point E. The circle that is drawn is the incircle.

To change the manipulative, first click on the arrow GeoGebra arrow button. menu button. Then click on the blue points and drag them to change the figure.

Table 2: Inscribing a circle in a triangle.

Cite this article as:

 McAdams, David E. How to Inscribe a Circle in a Triangle. 4/22/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/h/htinscribetriangle.html.

Image Credits

Revision History

4/22/2019: Update equations and expressions to new format. (McAdams, David E.)
7/16/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
7/3/2008: Initial version. (McAdams, David E.)

All Math Words Encyclopedia is a service of Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License