Induction
Pronunciation: /ɪnˈdʌk.ʃən/ ExplainMathematical induction is used to prove things about infinite sets. Mathematical induction starts with a few examples of an infinite series. If you can show that the claim is true for the first case, and that if the claim is true for an arbitrary case, then the claim is always true for the next case, you have proved that the claim about the infinite set is true.
Example
| Statement | Justification |
|---|---|
| State the claim. | |
We will show that
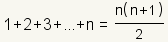 . .
| Statement of claim. |
| Show that the first case is true. | |
When
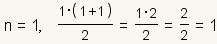
| Show the first case is true by substituting 1 for n. |
| Establish an arbitrary case. | |
Let
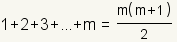
| Assume the mth case is true. |
| Show that, if the arbitrary case is true, then the next case must be true. | |

| Use the additive property of equality to add m + 1 to both sides. m + 1 is the next term. |
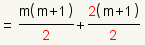
| Multiply the second term by 2 / 2 = 1. This uses the fact that 1 is the multiplicative identity. |
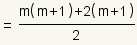
| Apply the distributive property of multiplication over addition and subtraction to combine the fractions. |
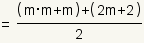
| Apply the distributive property of multiplication over addition and subtraction to distribute the numerator. |
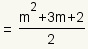
| Apply the commutative property of addition to combine the terms in the numerator. |
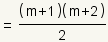
| Factor the numerator. |
Let
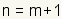
| 
|
Then
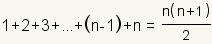
| QED. |
References
- McAdams, David E.. All Math Words Dictionary, induction. 2nd Classroom edition 20150108-4799968. pg 98. Life is a Story Problem LLC. January 8, 2015. Buy the book
- Cupillari, Antonella. Nuts and Bolts of Proof: An Introduction to Mathematical Proofs. 3rd edition. pp 48-57. Academic Press. August 15, 2005. Last Accessed 8/7/2018. Buy the book
- Gilbert, Jimmie; and Gilbert Linda. Elements of Modern Algebra. 6th edition. pp 63-70. Thomson, Brooks/Cole. 2005. Last Accessed 8/7/2018. Buy the book
More Information
- McAdams, David E.. Inductive Reasoning. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 3/12/2009. https://www.allmathwords.org/en/i/inductivereasoning.html.
Cite this article as:
McAdams, David E. Induction. 4/23/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/i/induction.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/23/2019: Updated equations and expressions to new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
8/6/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
12/30/2008: Added several vocabulary links. (McAdams, David E.)
11/26/2008: Changed equations to images. (McAdams, David E.)
8/9/2008: Changed equations to Hot_Eqn. (McAdams, David E.)
3/25/2008: Changed More Information to match current standard. (McAdams, David E.)
9/3/2007: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License