Integer

Pronunciation: /ˈɪn.tɪ.dʒər/ Explain

An integer is a whole number having no decimal part. An integer can be a positive whole number, a negative whole number, or zero. Examples of integers are 24, -142, and 0. The symbol for the set of natural numbers is a double struck capital N: ℕ. The definition of the set of integer in set notation is ℕ = {…, -3, -2, -1, 0, 1, 2, 3, …}.

In math, we can represent integers in ways that may not look like integers at first. For example, the fraction 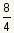can be reduced to 2, and so is an integer, even if it is represented by an improper fraction.

Another example is 5.00. While it is represented using decimal notation, it has a decimal part of 0, which is the same as no decimal part. However, in most computer based systems, 5.00 would be stored as a decimal number, not as an integer.

Here are some examples of numbers that are not integers: 5.2, 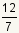(can not be reduced to a single whole number), p (has been proved to be irrational), and 0.3 (contains non-zero digits after the decimal point).

Properties of Integers

Property	Description
Associativity	The set of integers is associative with respect to addition, subtraction, multiplication and division.
Commutativity	The set of integers is commutative with respect to addition and multiplication. The set of integers is not commutative with respect to subtraction or division.
Additive identity	The additive identity for integers is 0.
Multiplicative identity	The multiplicative identity for integers is 1.
Closure	The set of integers is closed with respect to addition, subtraction and multiplication. The set of integers is not closed with respect to division.
Discrete	The set of integers is a discrete (not continuous) set.
Cardinality	The cardinality of the set of integers is ℵ0.
Table 1: Properties of the integers.

Understanding Check

Decide if each number represents an integer. Then click either 'integer' or 'not an integer'.

Number	Is an integer?
15	Integer Not an integer The number '15' is an integer. It has no digits to the right of the implied decimal point, is not an unreducible fraction, and does not represent an irrational number.
-6.4	Integer Not an integer The number '-6.4' is not an integer. It has nonzero digits to the right of the decimal point.
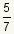	Integer Not an integer This number is not an integer. It is a nonreducible fraction.
-2.0000	Integer Not an integer The number '-2.0000' is an integer. It has no digits to the right of the implied decimal point, is not an unreducible fraction, and does not represent an irrational number. It can be written as '-2'.
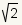	Integer Not an integer This number is not an integer. It represents an irrational number.
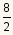	Integer Not an integer This number is an integer. The fraction reduces to the integer 4.
π	Integer Not an integer The number 'π' is not an integer. It represents an irrational number.
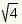	Integer Not an integer This number is an integer. The square root of 4 evaluates to 2.

References

1. McAdams, David E.. All Math Words Dictionary, integer. 2nd Classroom edition 20150108-4799968. pg 100. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. Jones, Burton. Elementary Concepts of Mathematics. pp 86-91. www.archive.org. MacMillan and Company. 1947. Last Accessed 8/7/2018. http://www.archive.org/stream/elementaryconcep029487mbp#page/n108/mode/1up/search/integer. Buy the book
3. Fish, Daniel W.. Robinson's Practical Arithmetic. pg 85. www.archive.org. Ivison, Blakeman, Taylor & Co.. 1881. Last Accessed 8/7/2018. http://www.archive.org/stream/numberstheory00robirich#page/84/mode/1up. Buy the book
4. Gilbert, Jimmie; and Gilbert Linda. Elements of Modern Algebra. 6th edition. pp 57-63. Thomson, Brooks/Cole. 2005. Last Accessed 8/7/2018. Buy the book

Cite this article as:

McAdams, David E. Integer. 4/23/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/i/integer.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/23/2019: Updated equations and expressions to new format. (McAdams, David E.)
3/22/2019: Fixed formatting issues. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
8/6/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
2/17/2010: Added "References". (McAdams, David E.)
11/25/2008: Changed equations to images. (McAdams, David E.)
8/11/2008: Added 'More Information' and 'Understanding Check'. (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)