Interpolation

Pronunciation: /ɪnˌtɜr.pəˈleɪ.ʃən/ Explain

Interpolation is a process for approximating the value of a function that is difficult to find. For example, say you want to approximate the value of .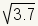

Step	Calculations	Description
1	Start with 1 and 4.	Find numbers larger and smaller than 3.7 that have easy to calculate square roots.
2		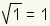The square root of 1 is 1.
3		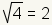The square root of 4 is 2.
4		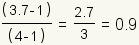What part of the way is 3.7 between 1 and 4?
5		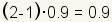About how much more is the square root of 3.7 than the square root of 1.
6		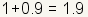Approximate the square root of 3.7. The actual value of the square root of 3.7 is about 1.9235.

References

1. McAdams, David E.. All Math Words Dictionary, interpolation. 2nd Classroom edition 20150108-4799968. pg 101. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. Rice, Herbert L.. The Theory and Practice of Interpolation. www.archive.org. Last Accessed 8/7/2018. http://www.archive.org/stream/theorypracticeof00rice#page/n5/mode/1up. Buy the book
3. Fraser, Duncan C.. Newton's Interpolation Formulas. vol LI pp 77-106,211-232 Oct 1918 - Aug 1919. www.archive.org. Reprinted from the Journal of the Institute of Actuaries. C. & E. Latton. Last Accessed 8/7/2018. http://www.archive.org/stream/newtonsinterpola00frasrich#page/n1/mode/2up. Buy the book
4. Steffenson, J. F.. Interpolation. 2nd edition. Reprint from 1950 edition. Dover Publications. March 17, 2006. Last Accessed 8/7/2018. Buy the book

Cite this article as:

McAdams, David E. Interpolation. 12/21/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/i/interpolation.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
8/6/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
2/18/2010: Added "References". (McAdams, David E.)
12/2/2008: Changed equations to images. (McAdams, David E.)
9/16/2008: Initial version. (McAdams, David E.)