Midpoint
Pronunciation: /ˈmɪdˌpɔɪnt/ ExplainA midpoint is a point equidistant between two points. The midpoint is on the line segment joining the two points and divides the line segment exactly in half. The exact mathematical definition of a midpoint is:
A midpoint M between points A and B is a point on the line AB such that AM = MB.
How to Construct a Midpoint
| Step | Illustration | Description |
|---|---|---|
| 1 | Start with the points A and B. | |
| 2 | Draw the line segment AB. | |
| 3 | Draw a circle with center at A and radius AB. | |
| 4 | Draw a circle with center at B and radius AB | |
| 5 | Mark one intersection of the two circles as point C and the other intersection of the two circles as point D. | |
| 6 | Draw the line segment CD. | |
| 7 | Mark the point of intersection of line segment AB and line segment CD as M. Point M is the midpoint. | |
| Table 1: Constructing a midpoint. | ||
How to Calculate a Midpoint in a 1-Dimensional Metric Space
|
Click on the blue points and drag them to change the figure. What happens is B is to the left of A? |
| Manipulative 8 - Calculating Midpoint in One Dimension Created with GeoGebra. |
The formula for a midpoint in a one dimensional space between
A and B is
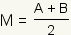 . Click on the
blue points in manipulative 1 and drag them to change the figure.
. Click on the
blue points in manipulative 1 and drag them to change the figure.
How to Calculate a Midpoint in a Metric 2-Dimensional Space
|
Click on the blue points and drag them to change the figure. |
| Manipulative 9 - Calculating Midpoint in Two Dimensions Created with GeoGebra. |
A midpoint divides the line segment exactly in half. This fact can be used
to figure out the formula for a midpoint of a line segment in a 2-dimensional
Euclidean space such as a Cartesian coordinate system. The x-coordinate of
the midpoint will be halfway between the x-coordinates of the two points, and
the y-coordinate of the midpoint will be halfway between the y-coordinates of
the two points. The formula for the midpoint of a line segment with end-points
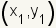 and
and
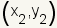 is
is
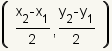 .
.
How to Calculating a Midpoint in a Metric n-Dimensional Space
The algorithm for calculating an endpoint in 2-dimensional
space can be generalized for n-Dimensional Space. Given two points
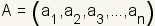 and
and
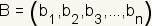 the midpoint is
the midpoint is
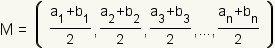 .
.
Proof: If M is the midpoint of AB, then AM = MB
This proof is a paragraph proof or informal proof.
The definition of the midpoint of a segment is that AM = MB. In other words, the lengths of the two segments are equal. By the definition of congruence, AM is congruent with MB if and only if AM and MB have the same measure. Since, by the definition of a midpoint, AM and MB have the same measure, AM = MB.
References
- McAdams, David E.. All Math Words Dictionary, midpoint. 2nd Classroom edition 20150108-4799968. pg 117. Life is a Story Problem LLC. January 8, 2015. Buy the book
More Information
- Euclid of Alexandria. Elements. Clark University. 9/6/2018. https://mathcs.clarku.edu/~djoyce/elements/elements.html.
Cite this article as:
McAdams, David E. Midpoint. 4/25/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/m/midpoint.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/25/2019: Changed equations and expressions to new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
9/3/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
3/22/2010: Added information on constructing a midpoint, calculating a midpoint in 1 dimension, and calculating a midpoint in n dimensions. (McAdams, David E.)
12/18/2009: Added "References". (McAdams, David E.)
10/7/2008: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License