Multiplication of Polynomials

Pronunciation: /ˌmʌl.tɪ.plɪˈkeɪ.ʃən ʌv ˌpɒl.əˈnoʊ.mi.əlz/ Explain

Multiplication of polynomials consists of multiplying each of the terms of the two polynomials, then adding the like terms.^[1] The degree of the resulting polynomial is the sum of the degrees of the polynomials being multiplied. The factors of the resulting polynomial are each of the factors of both polynomials being multiplied.

Example 1

Step	Equations	Description
1		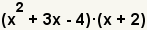These are the polynomials to multiply.
2		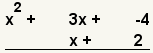Write the polynomials one under the other.
3		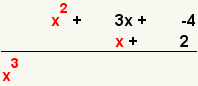Multiply the first term of the first polynomial and the first term of the second polynomial.
4		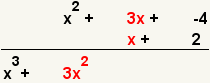Multiply the second term of the first polynomial and the first term of the second polynomial.
5		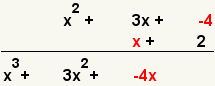Multiply the third term of the first polynomial and the first term of the second polynomial.
6		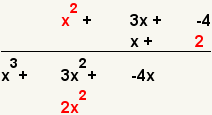Multiply the first term of the first polynomial and the second term of the second polynomial.
7		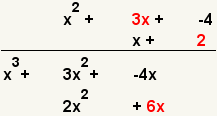Multiply the second term of the first polynomial and the second term of the second polynomial.
8		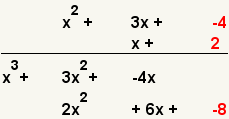Multiply the third term of the first polynomial and the second term of the second polynomial.
9		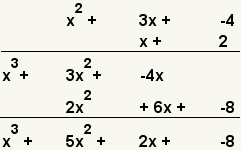Add the like terms of the products.
10		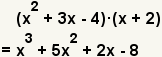Finished solution.
Example 1

References

1. McAdams, David E.. All Math Words Dictionary, multiplication of polynomials. 2nd Classroom edition 20150108-4799968. pg 121. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. Boyden, Wallace C., A.M.. A First Book in Algebra. pg 48. 1895. Last Accessed 9/2/2018. http://www.gutenberg.org/files/13309/13309-pdf.pdf. Buy the book

Cite this article as:

McAdams, David E. Multiplication of Polynomials. 12/21/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/m/multiplicationofpoly.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
9/4/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
12/18/2009: Added revision. (McAdams, David E.)
1/20/2009: Initial version. (McAdams, David E.)