Parallel Postulate

Pronunciation: /ˈpær.əˌlɛl ˈpɑs.tʃə.lət/ Explain

Click on the blue points and drag them to change the figure. Manipulative 1 - Parallel Postulate Created with GeoGebra.

The parallel postulate is the fifth postulate of Euclidean geometry. It states, That, if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles. Euclid. Elements, Book I.[2] Stated in simpler language, if the sum of the interior angles on the same side of a transversal of two lines is less than 180°, the two lines meet on that side.[3][5] If the sum of the angles is equal to 180°, the two lines do not meet, and so are parallel. If the sum of the angles is greater than 180°, the two lines meet on the opposite side. In modern geometry, this postulate is called the axiom of parallels and is stated differently: In plane α there can be drawn through any point A, lying outside of a straight line a, one and only one line that does not intersect line a. This line is called parallel to a through given point A.[4]

Cases of the Parallel Postulate

Diagram	Sum of interior angles	Lines meet …
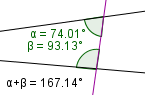	α + β < 180°	Lines meet on the same side as the interior angles.
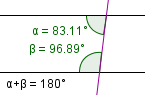	α + β = 180°	Lines do not meet. They are parallel.
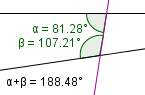	α + β > 180°	Lines meet on the opposite side of the interior angles.
Table 1: Cases of the Parallel Postulate.

Equivalences of the Parallel Postulate

There are a number of geometric properties that are equivalences of the parallel postulate. Two properties are equivalent if one implies the other. Some of the equivalencies of the parallel postulate are:

• The sum of the angles in every triangle is 180°.
• There exists a pair of similar, but not congruent, triangles.
• Every triangle can be circumscribed.
• If three angles of a quadrilateral are right angles, then the fourth angle is also a right angle.
• There exists at least two lines that are parallel.
• Two lines that are parallel to the same line are also parallel to each other.
• Given two parallel lines, any line that intersects one of them also intersects the other.
• Pythagorean theorem (A² + B² = C²).

Importance of the Parallel Postulate

The parallel postulate has been shown to be very important in the definitions of geometries. Because it is not intuitively obvious like the first four postulates, many mathematicians believed that the parallel postulate could be proved using the first four postulates. There were many attempts at this proof that were unsuccessful.

Starting in 1829, mathematicians switched from trying to prove the fifth postulate to exploring geometries that do not contain the parallel postulate. As a result, two valid geometries were discovered: hyperbolic geometry and elliptical geometry.

References

1. McAdams, David E.. All Math Words Dictionary, parallel postulate. 2nd Classroom edition 20150108-4799968. pg 134. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. Euclid. Elements. Book 1. Translated by Joyce, D. Clark University. Last Accessed 12/3/2018. https://mathcs.clarku.edu/~djoyce/elements/bookI/bookI.html. Buy the book
3. Casey, John, LL.D., F.R.S.. The First Six Books of the Elements of Euclid. pg 11. Translated by Casey, John, LL.D. F.R.S.. www.archive.org. Hodges, Figgis & Co.. 1890. Last Accessed 12/3/2018. http://www.archive.org/stream/firstsixbooksofe00caseuoft#page/11/mode/1up. Buy the book
4. Hilbert, David. The Foundations of Geometry. pg 7. Translated by Townsend, E. J., Ph. D.. The Open Court Publishing Company. 1950. Last Accessed 12/3/2018. http://www.gutenberg.org/files/17384/17384-pdf.pdf. Buy the book
5. parallel postulate. merriam-webster.com. Encyclopedia Britannica. Merriam-Webster. Last Accessed 12/3/2018. http://www.merriam-webster.com/dictionary/parallel postulate. Buy the book

More Information

• Euclid of Alexandria. Elements. Clark University. 9/6/2018. https://mathcs.clarku.edu/~djoyce/elements/elements.html.

Cite this article as:

McAdams, David E. Parallel Postulate. 4/27/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/p/parallelpostulate.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/27/2019: Changed equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/1/2018: Removed broken links, updated license, implemented new markup, updated geogebra app. (McAdams, David E.)
12/21/2009: Added "References". (McAdams, David E.)
10/24/2008: Initial version. (McAdams, David E.)