Reflexive Property of Equality
Pronunciation: /rɪˈflɛk.sɪv ˈprɒp.ər.ti ʌv ɪˈkwɒl.ɪ.ti/ ExplainThe reflexive property of equality for real numbers states that a number always equals itself: a = a.
Think of a mirror. When you look in a reflection in a mirror, everything on your right hand looks like it is on the left hand of the reflection. This is a good way to remember the reflexive property.
- Start with a.
- The equal sign is like a mirror. We will use it to reflect the a.
- Since the a is reflected across the equals, a = a. This is the reflexive property of equality.
Mnemonic What is a mnemonic?
Picture
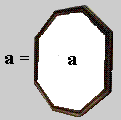 |
| Figure 1: a reflected as a = a. |
References
- McAdams, David E.. All Math Words Dictionary, reflexive property of equality. 2nd Classroom edition 20150108-4799968. pg 153. Life is a Story Problem LLC. January 8, 2015. Buy the book
- Gilbert, Jimmie; and Gilbert Linda. Elements of Modern Algebra. 6th edition. pp 49-50. Thomson, Brooks/Cole. 2005. Buy the book
Cite this article as:
McAdams, David E. Reflexive Property of Equality. 5/2/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/r/reflexivepropofequality.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
5/2/2019: Changed equations and expressions to new format. (McAdams, David E.)3/29/2019: Clarified wording. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/4/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
10/5/2008: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License