Solving an Equation

Pronunciation: /sɒlv.iŋ ən ɪˈkweɪ.ʒən/ Explain

Most math problems you will find in algebra involve solving equations. The idea is to find a solution to the !!!!!UNKNOWN REFERENCE equation.html!!!!!. A solution is a set of one or more values that, when substituted for the variable(s), make the equation true.

Solving equations is one of the most important math skills to learn. There are several classes of equations you will find in your studies:

• Single variable equations of degree one such as x + 3 = 2x - 4. The goal in solving these equations is to get the variable by itself on one side of the equals sign. What is left on the other side of the equation is the value of the variable.
• Single variable equations of degree two such as 2x² - 3x + 4 = 0. The quadratic formula is used for these quadratic equations.
• Two variable equations of degree one such as y = x - 4. These equations are linear equations. They can be graphed as a line. Linear equations with two variables have infinite solutions.
• Two equations of two variables, each being degree one such as y = 3x + 7, y = -x - 4. This is called a linear system. Linear systems have either no solution, one solution, or infinite solutions.

There are other types of equations to solve you may encounter in more advanced classes. These will not be discussed here.

Article Index

What Does it Mean to Solve an Equation?
Properties of Numbers Used to Solve Equations
Using Addition and Subtraction to Solve an Equation
Using Multiplication to Solve an Equation
Using Division to Solve an Equation
Using the Distributive Property to Solve an Equation
Solving an Equation Graphically
Solving a Quadratic Equation
Solving a Multiple Variable Equation

What Does it Mean to Solve an Equation?

To solve an equation is to find out what the equation tells one about the possible values of one or more variables. Take the equation x + 3 = 2x - 1. What does this equation tell one about the value of x? To find out, solve the equation.

Solving a one variable linear equation involves getting the variable on one side of the equals sign by itself. To do this one uses the properties of numbers.

Properties of Numbers Used to Solve an Equation

Property	Example	Description
Property of adding zero	Given a real number x; x + 0 = x	Zero added to any number equals the original number.
Addition property of equality	Given three real numbers a, b, and c; if a = b then a + c = b + c	If two numbers are equal, after adding the same value to each number, the sum remain equal.
Subtraction property of equality	Given three real numbers a, b, and c; if a = b then a - c = b - c	If two numbers are equal, after subtracting the same value from each number, the difference remain equal.
Property of multiplying by 1	Given a real number x; 1 · x = x	Any number multiplied by 1 equals itself.
Distributive property of multiplication over addition and subtraction	Give 3 real numbers a, b, and c; a ( b + c ) = ab + ac	A number multiplied by a sum is equal to the sum of the number multiplied by each term.
Transitive property of equality	Given three real numbers a, b, and c; if a = b and b = c then a = c	If two numbers are equal to the same other number, they are equal to each other.
Table 1: Properties of numbers used to solve an equation

How to Use Addition and Subtraction to Solve an Equation

Start with the equation x + 3 = 5. Since the goal is to get x by itself, one needs to do something about the 3 that is added to the x. To undo addition, use subtraction:

Step	Equation	Description
1	x + 3 = 5	Original equation
2	(x + 3) - 3 = 5 - 3	Subtraction property of equality.
3	(x + 3) + (-3) = 5 - 3	Definition of subtraction.
4	x + (3 + (-3)) = 5 - 3	Associative property of addition.
5	x + 0 = 2	Simplify both sides of the equation.
6	x = 2	Property of addition by zero.
7	(2) + 3 = 5 5 = 5	Check work by substituting the solution back into the equation.
Table 2: Solving x + 3 = 5.

Now start with the equation x - 2 = 1. Since addition undoes subtraction, use the addition property of equality.

Step	Equation	Description
1	x - 2 = 1	Original equation
2	(x - 2) + 2 = 1 + 2	Addition property of equality.
3	(x + (-2)) + 2 = 1 + 2	Definition of subtraction.
4	x + ((-2) + 2) = 1 + 2	Associative property of addition.
5	x + 0 = 3	Simplify both sides of the equation.
6	x = 3	Property of addition by zero.
7	(3) - 2 = 1 1 = 1	Check work by substituting the solution back into the equation.
Table 3: Solving x - 2 = 1.

How to Use Multiplication to Solve an Equation

Start with the equation x ÷ 3 = 6. Again, one wants to get the x by itself on one side of the equation. To undo multiplication, use division:

Step	Equation	Description
1	x ÷ 3 = 6	Original equation
2	(x ÷ 3) · 3 = 6 · 3	Multiplication property of equality.
3	x · (3 ÷ 3) = 6 · 3	Associative property of multiplication.
4	x · 1 = 18	Simplify both sides of the equation.
5	x = 18	Property of multiplication by 1.
6	18 ÷ 3 = 6 6 = 6	Check the work by substituting the solution back into the equation.
Table 4: Solving x ÷ 3 = 6.

How to Use Division to Solve an Equation

When using division to solve an equation, one must be sure to not divide by zero. Since division by zero is undefined, division by zero will give undesirable and incorrect results. Start with the equation 3x = 6.

< td>Check the work by substituting the solution back into the equation.

Step	Equation	Description
1	3x = 6	Original equation
2	(3x) ÷ 3 = 6 ÷ 3	Division property of equality.
3	(x · 3) ÷ 3 = 6 ÷ 3	Commutative property of multiplication.
4	x · (3 ÷ 3) = 6 ÷ 3	Associative property of multiplication.
5	x · 1 = 2	Simplify both sides of the equation.
6	x = 2	Property of multiplication by 1.
7	3 · 2 = 6 6 = 6
Table 5: Solving 3x = 6.

How to Use the Distributive Property to Solve an Equation

The distributive property of multiplication over addition and subtraction is used often to solve an equation. The example in table 6 uses the distributive property to remove parenthesis.

Step	Equation	Description
1	3(x - 4) = 3	Original equation
2	3 · x - 3 · 4 = 3	Distributive property of multiplication over addition and subtraction.
3	3x - 12 = 3	Simplify.
4	(3x - 12) + 12 = 3 + 12	Addition property of equality.
5	(3x + -12) + 12 = 3 + 12	Definition of subtraction.
6	3x + (-12 + 12) = 3 + 12	Associative property of addition.
7	3x + 0 = 15	Simplify.
8	3x = 15	Property of addition by zero.
9	x · 3 = 15	Commutative property of multiplication
10	x · 3 ÷ 3 = 15 ÷ 3	Division property of equality.
11	x · 1 = 5	Simplify both sides of the equation.
12	x = 5	Property of multiplication by 1.
13	3(5 - 4) = 3 3 · 1 = 3 3 = 3	Check the work by substituting the solution back into the original equation.
Table 6: Solving 3(x - 4) = 3.

The example in table 7 uses the distributive property to combine two terms containing the same variable.

Step	Equation	Description
1	3x = 2x + 3	Original equation
2	3x - 2x = 2x - 2x + 3	Addition property of equality.
3	3x - 2x = 0 + 3	Simplify.
4	3x - 2x = 3	Property of addition by zero.
5	x(3 - 2) = 3	Distributive property of multiplication over addition and subtraction.
6	x · 1 = 3	Simplify.
7	x = 3	Property of multiplying by 1.
8	3 · 3 = 2 · 3 + 3 9 = 6 + 3 9 = 9	Check the work by substituting solution back into the equation.
Table 7: Solving 3x = 2x + 3.

How to Solve an Equation Graphically

This section describes how to use a TI-83 or TI-84 graphing calculator to find the middle root of x³ - 0.5x² - 2x + 1. Most graphing calculators have a way to solve equations graphically. Check the user manual for your calculator.

1		Click the <CLEAR> button until you have a blank screen.
Step	Screen	Description
2		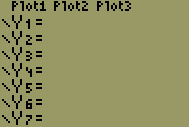Click the <Y=> button on the top row to view the graphing equation screen. If there are any equations showing, use the <CLEAR> key and the up and down arrows to erase all equations. Then click the up arrow key until it is in the top position.
3		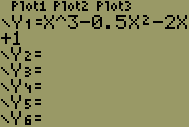Enter the equation x3 - 0.5x2 - 2x + 1 using the following keystrokes: <X,T,θ,n>, <^>, <3>, <->, <0>, <.>, <5>, <X,T,θ,n>, <x2>, <->, <2>, <x>, <+>, <1>.
4		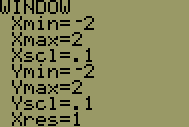Click on the <WINDOW> button to load the graphing window parameter screen. Use the number keys and the up and down arrow buttons to enter the window parameters as show in the screen image. When entering negative numbers, make sure to use the <(-)> key on the bottom row of the calculator. The key labeled <-> means subtract, not negate.
5		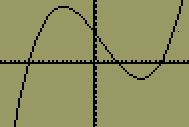Click the <GRAPH> button on the top row of the calculator. The graph of x3 - 0.5x2 - 2x + 1 will appear in the window you specified.
6		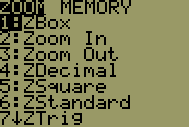Click the <ZOOM> button to see the zoom menu.
7		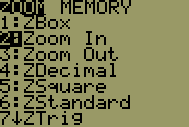Click the down arrow button once to select menu option 2-Zoom In.
8		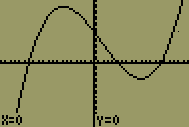Click the <ENTER> key on the bottom right corner of the calculator to return to the graph with the zoom option activated.
9		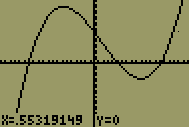Click the right arrow button until the cross hairs are near the middle intercept. The numbers at the bottom of the screen change to show you the coordinates of the cross hair.
10		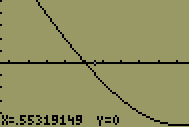Click the <ENTER> button to zoom in on the zoom coordinates.
11		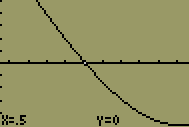Click on the left arrow button until the cross hairs are over the intercept. The zoom coordinates should be x = 0.5 and y = 0. The correct intercept is x = 0.5. You can click on the enter key again to make sure you are as close to the intercept as possible.
Table 8: Using the TI-83/84 calculator to find a root of x3 - 0.5x2 - 2x + 1.

How to Solve a Quadratic Equation

Quadratic equations in the form ax² + bx + c = 0 are solved using the quadratic formula: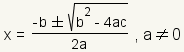
The a, b and c in the quadratic formula are the a, b and c in the quadratic equation. Because of the ± in the equation, a quadratic equation can have two solutions.

If the discriminant b² - 4ac is greater than zero, the quadratic equation has two real solutions. A real solution is a solution that is a real number. If the discriminant b² - 4ac is 0, the quadratic equation has one real solution. If the discriminant b² - 4ac is less than zero, the quadratic equation has two complex solutions. A complex solution is a solution that is a complex number.

Solving Using the Quadratic Equation

Step	Equation	Description
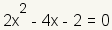		Equation to solve
1		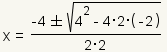Substitute a = 2, b = -4 and c = -2 into the quadratic formula.
2		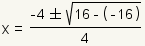Simplify exponents and multiplication inside the parenthesis.
3		Simplify the subtraction inside the parenthesis.
4		Since 32 = 16 · 2 and √16 · 2 = 4 √2, rewrite the radical as 4√2.
5		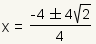Use the distributive property of multiplication over addition and subtraction to split the fraction into two fractions.
6		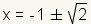Simplify each fraction.
7		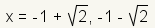Change the ± into two equations, one using + and the other using -. This quadratic equation has 2 solutions.
Table 9: Solving 2x2 - 4x - 2 = 0 using the quadratic formula.

How to Solve a Multiple Variable Equation

When solving a multiple variable equation, one solves for a variable. For example, given the equation x + y = 2, one can solve for the variable x or for the variable y. In this example we will solve for y.

x + y = 2	Equation to solve in standard form
x + y - x = 2 - x	Subtract x from both sides.
y = 2 - x	Simplify the left side of the equation.
y = -x + 2	Put equation in slope/intercept form.
Table 10: Solving for y

References

1. McAdams, David E.. All Math Words Dictionary, solve. 2nd Classroom edition 20150108-4799968. pg 168. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. Jones, Burton. Elementary Concepts of Mathematics. pp 141-144. www.archive.org. MacMillan and Company. 1947. Last Accessed 12/13/2018. http://www.archive.org/stream/elementaryconcep029487mbp#page/n162/mode/1up/search/equations. Buy the book

Cite this article as:

McAdams, David E. Solving an Equation. 5/13/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/s/solvingequation.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

5/13/2019: Changed equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/10/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
7/25/2008: Initial version. (McAdams, David E.)