System of Equations

Pronunciation: /ˈsɪs.təm ʌv ɪˈkweɪ.ʒənz/ Explain
y = x2 - 3
y = 2x + 1
Figure 1: A system of equations

A system of equations is a set of equations that are taken to be simultaneously true. A system of equations is also called simultaneous equations. If a system of equations contains only linear equations is a linear system.

A system of equations may have no solution. This means that there are no values for which all the equations are true at once. A system of equations may have one or more solutions. The solution(s) of the system of equations are any values for which all the equations are simultaneously true.

Visualizing a System of Equations

Click the line and parabola and drag them to change the figure.

Move the line and parabola so that there are no soultions, one solution and two solutions. With a line and parabola, can there be more than two solutions? Why?
Manipulative 1 - Simultaneous Equations Created with GeoGebra.

A system of equations can be visualized by graphing the equations. The solution(s) of the system are the points of intersections of the curves. If the graphs of the equations do not intersect, the system has no solutions.

The figure in manipulative 1 shows two simultaneous equations. The parabola is green and the line is blue. The red points are the points of intersection. The values of the red points are the solutions to the system. Click on the line and the parabola and drag them to change the figure.

Discovery

What is the greatest number of solutions that can be found for a system consisting of a line and a parabola?

How to Solve a System of Equations Using Substitution

A system of equations can often be solved by substitution. One variable is replaced by an expression equal to that variable. Take the system of equations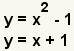
y=x^2-1,y=x+1

StepEquationsDescription
1y=x^2-1,y=x+1 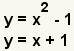These are the simultaneous equations to solve.
2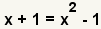x+1=x^2-1 Use the substitution property of equality to substitute x + 1 in for y.
3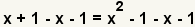x+1-x-1=x^2-1-x-1 Since the resulting equation in step 2 is a quadratic, we will be using the quadratic formula to solve it. The quadratic formula requires a zero be on one side of the equation. Use the additive property of equality to add -x - 1 to both sides.
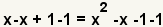x-x+1-1=x^2-x-1-1Use the associative property of addition to get like terms next to each other.
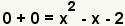0+0=x^2-x-2Combine like terms.
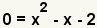0=x^2-x-2Use the additive property of zero to simplify the left side of the equation.
4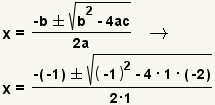x=((-b+-square root(b^2-4*a*c))/(2*a) implies x=((-(-1)+-square root((-1)^2-4*1*(-2)))/(2*1)Apply the quadratic formula with a = 1, b = -1 and c = -2.
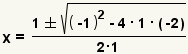x=((1+-square root((-1)^2-4*1*(-2)))/(2*1)Use the definition of negation to simplify the double negative.
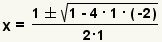x=((1+-square root(1-4*1*(-2)))/(2*1)Simplify the exponent.
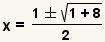x=((1+-square root(1+8))/2Simplify multiplication and division.
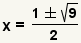x=((1+-square root(9))/2Simplify addition and subtraction.
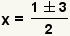x=(1+-3)/2Simplify the square root.
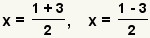x=(1+3)/2, x=(1-3)/2Split the plus or minus into two equations.
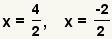x=4/2, x=(-2)/2Split addition and subtraction.
x=2, x=-1Simplify the fractions. These are the possible values of x.
5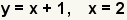y=x+1,x=2Use the substitution property of equality to substitute 2 in for x.
y=2+1Perform the substitution.
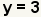y=3Simplify the addition.
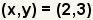(x,y)=(2,3)One solution of the system is the ordered pair (2, 3).
6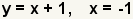y=-1+1Use the substitution property of equality to substitute -1 in for x.
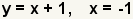y=-1+1Perform the substitution.
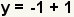y=0Simplify the addition.
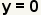(x,y)=(-1,0)One solution of the system is the ordered pair (-1 ,0).
Table 1: Solving simultaneous equations

References

  1. McAdams, David E.. All Math Words Dictionary, system of equations. 2nd Classroom edition 20150108-4799968. pg 174. Life is a Story Problem LLC. January 8, 2015. Buy the book

More Information

  • McAdams, David E.. Linear System. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 3/12/2009. https://www.allmathwords.org/en/l/linearsystem.html.

Cite this article as:

 McAdams, David E. System of Equations. 5/7/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/s/systemofequations.html.

Image Credits

Revision History

5/7/2019: Changed equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/10/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra app. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
2/10/2009: Initial version. (McAdams, David E.)

All Math Words Encyclopedia is a service of Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License